WisFaq!

Re: Hypothese toetsen

Super bedankt! Maar dat had ik inderdaad al gedaan, het binomaiaal gedeelte met het significantieniveau (significatieniveau was 0,02). Maar mijn probleem was dus de normaal verdeling, hebben jullie daar ook een oplossing:).
Alvast bedankt!

Wietske
4-2-2008

Antwoord

We hebben te maken met een binomiaal verdeling:

X:aantal keren rood
n=100
p=¹⁸/₃₇
X~Bin(100,¹⁸/₃₇)
Gevraagd: Wat is k zodat P(X$\leq$k)$\leq$0.02

Benaderen met de normale verdeling:
X·~Norm($\mu$,$\sigma$)
$\mu$=n·p=100·¹⁸/₃₇$\approx$48.6
$\sigma$=√(n·p(1-p))=√(100·¹⁸/₃₇·¹⁹/₃₇)$\approx$5.0
Gevraagd: P(X·$<$k)$\leq$0.02 met X·~Norm(48.6,5.0)

Met je GR en invNorm:



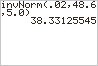
k=38.3

Rekeninghoudend met de continuiteitscorrectie kom je dan uit op een grenswaarde van 37. Dus bij 37 keer rood (of minder) mag je H₀ verwerpen.

Ter controle:

..en dat lijkt me dan wel zo'n beetje het idee...

WvR
4-2-2008