y=2x-4
(2x-4)2=4x
4x2-16x+16=4x
4x2-20x+16=0
x2-5x+4=0
(x-1)(x-4)
x=1 of x=4
Snijpunten (1,-2) en (4,4)
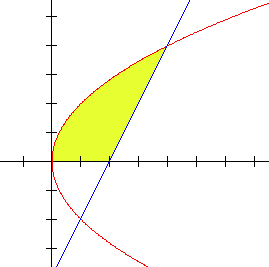
Oppervlakte onder parabool/rechte
WvR
1-7-2007
Hallo,
Ik had een vraagje over het berekenen van een oppervlakte:
De oppervlakte van de kleinste vlakke figuur die begrensd wordt door de parabool: y2= 4x, de rechte y= 2x-4 en de x-as bedraagt:
A: 3 B 5/2 C: 7/3 D:4Ö2/3
Ik ben begonnen met de snijpunten te zoeken van de parabool en de rechte. Met behulp van discriminant kom ik uit op -2 en 4. Ik veronderstel dat het gedeelte daartussen de oppervlakte is.
Dus dan bekom ik:
opp= òy2/4 - y/2-2 met als bovengrens 4 en ondergrens -2)
Om dan verder op te lossen met integratie door splitsing.
Is deze methode juist of zie ik toch ergens iets boven het hoofd. Want ik kom na uitwerking geen enkele van de meerkeuze oplossingen uit:P
Bedankt!Nick
1-7-2007
y2=4x
y=2x-4
(2x-4)2=4x
4x2-16x+16=4x
4x2-20x+16=0
x2-5x+4=0
(x-1)(x-4)
x=1 of x=4
Snijpunten (1,-2) en (4,4)
Oppervlakte onder parabool/rechte
WvR
1-7-2007
#51560 - Integreren - 3de graad ASO