WisFaq!

Verloop van functies

Bereken de oppervlakte van de grootst mogelijke rechthoek die kan ingeschreven worden in een halve cirkel met straal r.

jo
17-6-2007

Antwoord

Ik neem aan dat je zoiets bedoelt als:



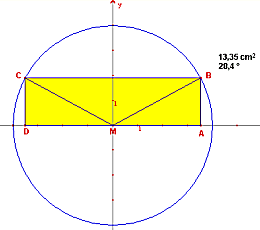
B is een willekeurig punt op de halve cirkel met straal r. Met a=ĐAMB geldt:

x_B=r·cosa
y_B=r·sina

Zodat voor O(a)=oppervlakte(ABCD) geldt:

O(a)=4·¹/₂·r·cosa·r·sina=2r²·sina·cosa
O'(a)=4r²·cos²a-2r²

4r²·cos²a-2r²=0̃a=¹/₄p+k·¹/₂p

De maximale oppervlakte is 2r²·sin¹/₄p·cos¹/₄p=2r²·¹/₂=r²

WvR
18-6-2007