WisFaq!

Re: Re: Getallen bepalen

Ok, maar ik kan de link niet leggen tussen: (n+m)^m en n^m dat die dezelfde rest hebben bij deling door m, en dat m dan een deler moet zijn van 1413.

De getallen heb ik gewonden: m = 3, dan is n = 11 en m kan ook 9 zijn, maar dan is n geen positief geheel getal meer.

Jeroen
25-4-2007

Antwoord

Beste Jeroen,

Mooi gevonden. 1413 = 3*3*157 dus de delers zijn 3, 9, 157 en 471. Die laatste twee kunnen ook. Maar ook dan zul je geen positieve gehele n vinden.

Over de aanpak maar even een voorbeeldje:

Je hebt: (n+m)^m = n^m + 1413

probeer je nu eens m=7 en een aantal getallen voor n. Dan krijg je dit:


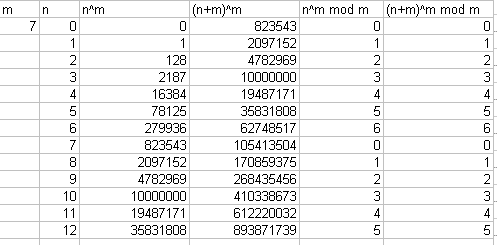
Je ziet: (n+m)^m is veel groter dan n^m maar als je de rest neemt bij delen door m zijn ze weer hetzelfde. Het maakt niet uit welke waarde je voor n invult. Kijk je nu weer naar je vergelijking dan zie je dat het alleen maar mogelijk is dat die twee dezelfde rest hebben als 1413 (bij delen door m) een rest van 0 heeft. En dat betekent dat m een deler moet zijn van 1413. Voor m=7 is dat niet het geval: 1413 mod 7 = 6. Dus weet je zonder dat je een n hoeft uit te proberen dan m=7 geen oplossingen zal geven.

os
25-4-2007