P(k$>$4)=1-P(k$\leq$4)
Dus:
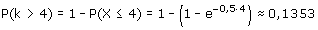
Nou ja...

Zie 7. Negatief exponentiŽle verdeling
WvR
14-12-2006
Een satelliet heeft 5 zonnepanelen. Ieder zonnepaneel heeft een levensduur die kan worden beschreven door een negatief-exponentiŽle verdeling met mu = 0,5. Dus de gemiddelde levensduur van een paneel is 1/0,5 = 2 jaar. Zodra 3 panelen zijn uitgevallen, houdt de satelliet op te functioneren.
a) Hoe groot is de kans dat een willekeurig zonnepaneel na 4 jaar nog functioneerd?
Ik dacht zelf aan dit maar het klopt niet.
P(k≥4) mu=0.5
1-P(k≤3) mu 0.5
Ik weet dat het antwoord 0.1353 moet zijn (antwoordenboek) maar daar wordt geen uitleg gegeven
b) Hoe groot is de kans dat de satelliet na 4 jaar nog functioneerd? We gaan ervan uit dat de levensduren van de panelen onderling onafhankelijk is.
En dit is de kans van de vorige vraag tot de macht 3 toch????
Gerard
12-12-2006
Moet het niet zijn:
P(k$>$4)=1-P(k$\leq$4)
Dus:
Nou ja...
Zie 7. Negatief exponentiŽle verdeling
WvR
14-12-2006
#48054 - Kansverdelingen - Student hbo