WisFaq!

Aantonen Formule

Dag beste,
ik moet de volgende formule aantonen.

Je weet:
An · sin ( nωt ) + Bn · cos ( nωt )
= Xn · sin ( nωt + $\Phi$n )
= Xn · ( sin ( nωt ) · cos ( $\Phi$n ) + cos ( nωt ) · sin ( $\Phi$n ))

een coëfficientenvergelijking geeft:
An = Xn · cos ( $\Phi$n )
en
Bn = Xn · sin ( $\Phi$n ))

uit de bovenstaande volgt een tweeede gedaante van de Fourrier reeks:
f(t) = ( B0 / 2 ) + ∑ ( n = 1 onder en ∞ boven) ( Xn · sin ( nωt + $\Phi$n )

Waarin : Xn = √( An² + Bn² )
tg $\Phi$n = Bn / An

Alvast bedankt,
Bart

Bart
20-11-2006

Antwoord

asinx+bcosx
= √(a²+b²).(a/√(a²+b²)·sinx + b/√(a²+b²)·cosx)

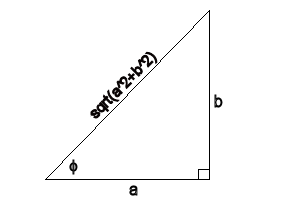
Nu kun je de a, de b en de √(a²+b²) uitzetten in een rechthoekige driehoek, waarbij de √(a²+b²) natuurlijk de schuine zijde is.
En bijv. de aanliggende zijde = a.
dan geldt dat cos$\phi$=a/√(a²+b²) en sin$\phi$=b/√(a²+b²)



dus asinx+bcosx
= √(a²+b²).(cos$\phi$sinx + sin$\phi$cosx)
= √(a²+b²).sin(x+$\phi$)

dit zou je een eindje verder moeten helpen.

groeten,
martijn

mg
20-11-2006