WisFaq!

Vermenigvuldigen t.o.v. de y-as

hallo,
ik heb een vraag. f(x) = ¹/₄x³
de grafiek van f wordt met ¹/₂ vermenigvuldigd ten opzichte van de y-as. zo onstaat grafiek van g en g'. geef de formules van g en g'.
hoe kan ik nou deze som aanpaken en wat is verschil bij het berekenen van vermenigvuldiging ten opzichte van y-as en x-as. alvast bedank!

Faiz
15-10-2002

Antwoord

Ik neem aan dat je het hebt over de functie:

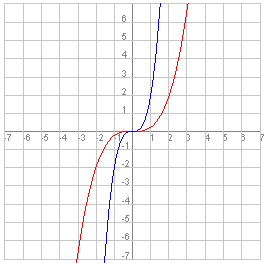
f(x)=¼x³

Als je f vermenigvuldigt met een ½ t.o.v. de y-as, dan gebeurt er 'iets' met de x-waarden. De grafiek wordt als het ware ingekrompen... of anders gezegd de x-waarden gaan 'twee keer zo hard..'. Concreet betekent dit dat je voor g kunt schrijven:

g(x)=¼(2x)³=¼·8·x³=2x³



Hoe zit dat dan met de afgeleide?
f'(x)=³/₄x²
g'(x)=6x²

Hadden we dat kunnen zien aankomen? Ik bedoel: kan je, als je de afgeleide kent van f, de afgeleide van g afleiden op grond van de vermenigvuldiging t.o.v. de y-as?

Het antwoord is natuurlijk: ja!
In je boek staat misschien wel ergens:

[f(cx)]'=c·f'(cx)

In ons voorbeeld zou dat betekenen dat:
g'(x)=2·³/₄(2x)²=2·³/₄4x²=6x²

Bovenstaande regel is eigenlijk niet heel erg moeilijk om te begrijpen, want differentieer f(cx) maar eens:
[f(cx)]'=f'(cx)·c (vanwege de kettingregel!)

Nog even over het verschil tussen vermenigvuldigen t.o.v. de y-as en vermenigvuldigen t.o.v. de x-as. Bij de eerste vermenigvuldiging veranderen voor alle punten van de grafiek de x-coördinaten, dus je moet iets 'doen' met de x in het functievoorschrift. Bij vermenigvuldigen t.o.v. de x-as veranderen van alle punten de grafiek de y-coördinaten, dus doe je iets met de y, of beter met de functiewaarde.

Zelf onthoud ik altijd zo: als je iets met x moet doen, dan doe je precies het tegenovergestelde van wat je zou verwachten (denk aan 3 naar rechts dan wordt x juist x-3 en vermenigvuldig met 2 t.o.v. de y-as... x wordt dan x/2). En als je iets met y doet, dan doen je gewoon wat er staat (4 omhoog dan y=...+4 of vermenigvuldig met 2 t.o.v. de x-as dan wordt y=... gewoon y=2·...).

WvR
15-10-2002