WisFaq!

Aantonen Formules

Dag beste,

Ik moet de volgende Formules aantonen:

1. ∫sin(kωt) · sin(mωt) dt = 0 voor k is niet gelijk aan m
= T/2 voor k=m
Met k, m element van $\mathbf{Z}$

2. . ∫cos(kωt) · cos(mωt) dt = 0 voor k is niet gelijk aan m
= T/2 voor k=m
Met k, m element van $\mathbf{Z}$

3. ∫sin(kωt) · cos(mωt) dt = 0
Met k, m element van $\mathbf{Z}$

Met bij elke ∫ staat T boven aan een 0 onderaan.


Alvast bedankt.

bart
12-11-2006

Antwoord

Dag Bart,

voor dit probleem heb je onder meer de volgende identiteiten nodig:


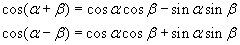
Wanneer je deze 2 identiteiten bij elkaar optelt, krijg je


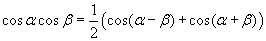
En als je ze van elkaar aftrekt krijg je


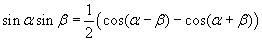
Met deze wetenschap leidt jouw eerste integraal tot:


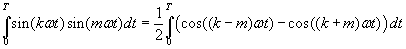
Dit kan opgesplitst worden in 2 situaties. ten eerste wanneer k¹m


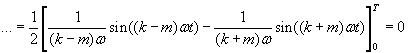
En ten tweede wanneer k=m :


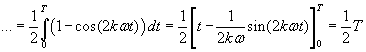
Nu kun je zelf met bovenstaande informatie bedenken hoe het zit met je tweede integraal.

En als je tot slot dan nog beschikt over de identiteiten

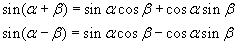
Dan kun je ook de derde integraal aan.

groeten,

martijn

mg
12-11-2006