WisFaq!

FLOOR functie

Hallo,

Ik hoop dat jullie me met het volgende kunnen helpen.
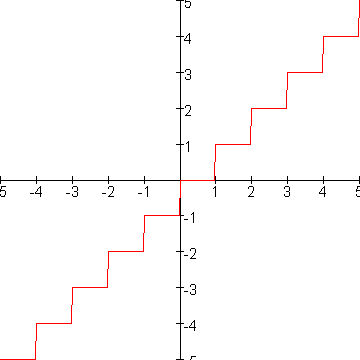
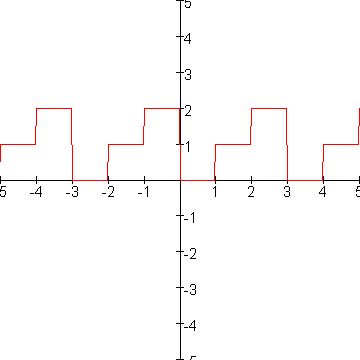
Ik moet bewijzen dat -2 [x] - 3 [x/3] 0.
waar n Î.

De tip die is gegeven is om x te schrijven als x=3n+d waar 0d3. Zo mijn eerste stap is om deze waarde te substitueren. Echter alles wat ik daarna probeer werkt niet. Ik hoop dat jullie me kunnen helpen.

Vriendelijke groet

Herman de vries
17-10-2006

Antwoord

Volgens mij klopt er het een en ander niet in je vraag.
Volgens mij zou moeten gelden 0floor(x)-3floor(x/3)2.
Verder lijkt het me handiger om x te schrijven als x=3n+d met 0d3.

Eerst maar eens een definitie van de functie floor: floor(x) is het grootste gehele getal dat niet groter is dan x.
In plaatjesvorm:



In formulevorm: als nxn+1 (met n een geheel getal) dan is floor(x)=n.

Nu naar jouw opgave.
Eerst maar eens een grafiek van floor(x)-3floor(x/3)



Je ziet een grafiek met periode 3.
Vandaar dat het handig is x te schrijven als 3n+d met n geheel en 0d3.
Bekijken we eerst 3floor(x/3)=3floor(n+d/3).
Omdat 0d3 geldt 0d/31. Dus 3*floor(n+d/3)=3n.
Nu floor(x)=floor(3n+d).
Als 0d1 dan is floor(3n+d) gelijk aan 3n.
Als 1d2 dan is floor(3n+d) gelijk aan 3n+1.
Als 2d3 dan is floor(3n+d) gelijk aan 3n+2.

Hier trekken we dan 3floor(x) vanaf en dat was gelijk aan 3n.
We houden dus over: 0, 1 of 2 afhankelijk van de waarde van d.

hk
19-10-2006