Je moet de veranderlijken scheiden, bijvoorbeeld alles in p naar het linkerlid en de rest naar het rechterlid.
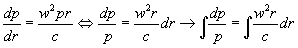
Kan je het nu afmaken?
mvg,
Tom
td
1-3-2006
Hoi,
Het gaat om deze gegeven vergelijking:
dp/dr = (w^2*p*r)/C
Met p is een druk, r is een radius en w en C zijn constanten.
Nu moet met de gegeven grenswaarden p(r=0) = p0, de functie p(r) gevonden worden.
Nu dacht ik dit in eerste instantie te doen door (w^2*p*r)/C te integreren naar r. In dat geval zou het worden:
p(r) = (p*w^2*r^2)/(2*C)
Maar dit kan natuurlijk niet omdat in de functie p(r) nu p zelf zit.
Hoe moet ik dit oplossen?
Het antw. is overigens: p(r) = p0*EXP[(w^2*r^2)/(2*C)]
Vriendelijke groeten,
Sil
Sil
1-3-2006
Beste Sil,
Je moet de veranderlijken scheiden, bijvoorbeeld alles in p naar het linkerlid en de rest naar het rechterlid.
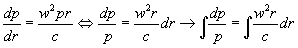
Kan je het nu afmaken?
mvg,
Tom
td
1-3-2006
#43920 - Integreren - Student hbo