Je werkt hier met een sinus en cosinus, die beschrijven een volledige kromme als de parameter t een periode van je componenten doorloopt. Als de 4t van de cosinus 2$\pi$ doorloopt dan moet t $\pi$/2 doorlopen.
De formule voor een booglengte L van een vlakke kromme geparametreerd in t met grenzen 0 en 2$\pi$ is dan:
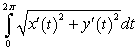Voor alle duidelijkheid, dat is de wortel uit de som van de kwadraten van de afgeleiden van x en y naar t.Je zal dan waarschijnlijk wel wat met goniometrisch formules moeten prutsen om van die wortel af te geraken zodat het integreerbaar is. Als dat niet lukt laat je maar iets horen
mvg,
Tom
td
2-7-2005