 :
:Hoe los je dit bij de poissonverdeling op:
Ik wil nu weten wat is l (de verwachtingswaarde) in de volgende formule:
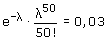
Hoe kan ik de l berekenen? Hopelijk is het nu duidelijk genoeg... :)
Yolan
4-5-2005
Okay.. ik zal proberen mijn vraag duidelijker te stellen:
Hoe los je dit bij de poissonverdeling op:
Ik wil nu weten wat is l (de verwachtingswaarde) in de volgende formule:
Hoe kan ik de l berekenen? Hopelijk is het nu duidelijk genoeg... :)Yolan
4-5-2005
Veel beter, vooral mijn formule is erg duidelijk...
Een mogelijkheid is om met onderstaand scriptje net zolang te prutsen totdat je de goede kans krijgt. Begin bijvoorbeeld eens met 40.
Dat blijkt dan te klein... 45 is te groot... 42.5 lijkt aardig te kloppen!
Een andere mogelijkheid is om je GR (TI83+) in te zetten. Via DIST kan je daar de Poissonverdeling vinden. Je kunt met Poissonpdf( dezelfde werkwijze volgens als boven...
Poissonpdf(40,50)®0,01770...
Poissonpdf(50,50)®0,05632...
Poissonpdf(45,50)®...
Als je niet van 'inklemmen' houdt kan je ook het volgende doen:
Zet bij Graph deze functie neer:
Y1=Poissonpdf(X,50)
Y2=0,03
WINDOW [40,60]x[0,.5]
...en dan met CALC en intersect kan je aflezen:
X=42,5531...
Algebraisch oplossen lijkt me in dit geval niet echt een optie...
Hopelijk is het zo duidelijk genoeg...
P.S.
Met je GR kom je er dan achter dat er nog een oplossing is! Mag je zelf zoeken!
WvR
4-5-2005
#37625 - Kansverdelingen - Leerling bovenbouw havo-vwo