WisFaq!

Bewijs met omtrekshoeken en middelpuntshoeken

Gegeven is een cirkel c(M,r). Op de cirkel liggen willekeurig een A B en C. We construeren nu de lijnstukken [MB] en [MC] en [AB] en [AC]. Het snijpunt van [AC] en [BM] noemen we X. Nu moeten we bewijzen dat hoek C + hoek A = hoek B

Maar hoe?

stijn
10-2-2005

Antwoord

Ik heb in de tekening de punten Y en Z ook geconstrueerd.

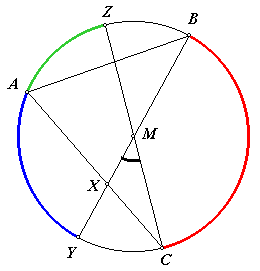
Je schrijft immers zelf, dat het over omtrekshoeken gaat.
En: "een omtrekshoek is gelijk aan de helft van de boog waarop hij staat".
En dan kan je de bogen uitdrukken in de hoeken.
Ik stel maar wat vragen.
- Waarom is bg(CY) = bg(BZ)?
- Waarom is bg(AZ) = 2C (C = hoek ACZ)? (*)
- Waarom is bg(BZ) = 180 - 2B - 2C (*)
- Hoe groot is bg(CY) uitgedrukt in A?
Lukt het nu verder?
Overigens, bij mij geldt nu: A = B + C.

(*) Naar aanleiding van een reactie op deze vraag.
Hier is gebruik gemaakt van de stelling:
een omtrekshoek is gelijk aan de helft van de cirkelboog waarop die hoek staat.
Het is een bekende stelling waarvan het bewijs in de meeste meetkundeboeken wel te vinden is.

dk
10-2-2005