WisFaq!

Dubbele integraal

Beste,
Ik zou de volgende functie moeten integreren over een begrensd gebied.
f(x,y)= (sin y)/y
Het integratiegebied wordt gegeven door volgende rechten:
y = x en y = √x
Als grenzen heb ik gevonden:
0 $<$= x $<$= 1
x $<$= y $<$= √x
Dus moet ik eerst over y integreren en als laatste over x. Nu zit ik vast bij de integraal van (sin y)/y. Hoe moet ik dit eigenlijk integreren? Heb geprobeerd met 2 keer partieel te integeren maar ik kom er niet uit.

Zouden jullie me kunnen verder helpen?
Bedankt,

Joachim

Joachim denil
6-1-2005

Antwoord

In eerste instantie kan je het gebied opvatten als Type I (zie een dubbelintegraal over een oppervlak) Je krijgt dan:



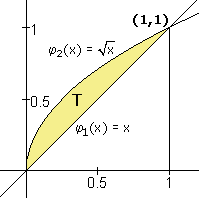
Dit leidt dan tot de volgende integraal:



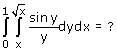
...en dat lukt niet erg...

In zo'n geval kan je eens proberen met de volgorde van integratie veranderen.

Je kunt het gebied ook opvatten als een gebied van Type II. In dit geval levert dat:



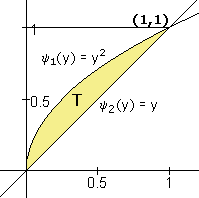
Met de volgende integraal:



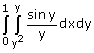
Het was natuurlijk een gebied van Type III en dan heb je nog keus! In het laatste geval gaat het allemaal een stuk makkelijker! Probeer 't maar eens!

WvR
6-1-2005