Ik heb een figuur bestaande uit een n aantal coordinaten.
Ik wil de afmetingen hebben van de klenst mogelijke rechthoek waar deze figuur in past. En ik wil de figuur met de rechthoek zo gedraaid hebben dat deze evenwijdig ligt aan mijn papier.
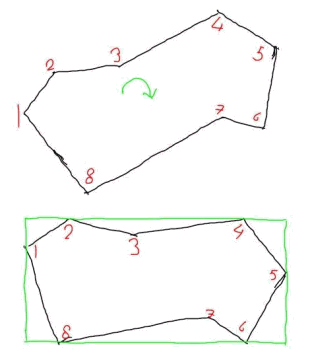
Ik wil hier graag een programmatje voor schrijven in VB maar Hoe moet ik hier mee beginnen?Stephan
24-10-2004
Hallo Stephan,
Het vraagstuk waar je mee komt is een minimalisatie-probleem. Dan moet je allereerst goed eenduidig formuleren wat de doelfunctie moet zijn. Je zegt dat je de 'kleinst mogelijke rechthoek' wilt vinden. Maar hoe definieer je klein/groot, m.a.w. welke maat gebruik je:
- de langste zijde?
- misschien wel juist de kortste zijde?
- de lengte van de diagoneel?
- de som van de zijden (dus: de omtrek)?
- de oppervlakte van de rechthoek?
- of misschien wel nog iets anders?
Ik ga er maar vanuit dat je de rechthoek wilt met de kleinste oppervlakte. Je noemt vooral het probleem om de punten over de juiste hoek te draaien. Als je eenmaal de juiste hoek hebt gevonden dan is het bepalen van de minimale rechthoek (met horizontale en verticale zijden) eenvoudig door het bepalen van de kleinste en grootste X- en Y-waarden. Ik heb twee ideeën voor je om het probleem van het vinden van de optimale hoek op te lossen, een relatief eenvoudige benadering of een constructie om de exacte oplossing te vinden:
BENADERING:
Je begint kennelijk met een 2D puntenwolk. Daarvan kun je het middelpunt bepalen door de X- en Y-waarden te middelen. Een maat voor de spreiding zijn de variantie $<$X2$>$-$<$X$>$2, $<$Y2$>$-$<$Y$>$2 en de covariantie $<$XY$>$-$<$X$><$Y$>$. Laten we even beginnen met het gemiddelde overal van af te trekken, zodat we er in het vervolg van uit kunnen gaan dat $<$X$>$=0=$<$Y$>$, zodat o.a. $\sigma$X = √$<$X2$>$ en $\sigma$Y = √$<$Y2$>$. Nu zouden we willen weten op welke manier $<$X2$>$ en $<$Y2$>$ veranderen onder rotaties. Enig uitwerken laat zien dat je daarvoor 'gewoon' de basistransformatie op de matrix
uit moet voeren.
M.a.w. als je deze matrix op hoofdassen brengt, dan heb je de rotatie gevonden waarvoor de covariantie nul en het product $\sigma$X$\sigma$Y minimaal is (dat laatste vergt ook nog wat uitwerken om het echt te bewijzen). Welnu, daarvoor kan ik je nu de formule geven; de hoek j waarover je moet draaien wordt gegeven door:
tan(j) = $\beta$ ± √($\beta$2+1), met $\beta$=($<$X2$>$-$<$Y2$>$)/(2 $<$XY$>$).
Daarvoor is het product van de standaarddeviaties, $\sigma$X$\sigma$Y, minimaal. Dat is weliswaar niet helemaal de norm die jij zou hebben gekozen, maar als je deze hoek eenmaal hebt kun je de door jou gewenste rechthoek makkelijk bepalen door de kleinste en grootste waarden van X en Y (na rotatie natuurlijk) te bepalen. Als er geen al te rare uitschieters in je puntenwolk zitten zal dit al een aardig eind in de richting komen, omdat de gevonden hoek j al wel ongeveer de optimale zal zijn.
EXACT:
De doelfunctie die je eigenlijk in gedachten hebt is Opp = (maxX - minX) (maxY - minY), het product van de minimale zijden in horizontale en verticale richting. Om hiervoor de optimale hoek exact te bepalen stel ik het volgende meer-stappen plan voor:
Stap 1: Bepaal het convexe omhulsel van je puntenwolk. M.a.w. zoek de punten die de buitenrand van jouw puntwolk weergeven als je ze met elkaar verbind, bovendien moet je ze op volgorde (rechtsom of linksom) nummeren, in feite zoals in het plaatje dat je hebt meegestuurd, maar dan zonder de punten 3 en 7 omdat die toch al binnen de lijn 2-4 resp. 6-8 vallen. Op die manier zorg je ervoor dat je je niet bezig houdt met punten die er toch niets toe doen. Een manier om hiervoor een algoritme te maken zou zijn om eerst het punt met (bijvoorbeeld) de kleinste X-waarde te zoeken. Daarna ga je dan vanuit dat punt alle lijnen naar de andere punten bekijken en kiest de lijn die het meest naar boven resp. het meest naar onderen gaat (grootste resp. kleinste richtingscoefficient, of: min/max van de hoek t.o.v. een zekere referentielijn (waarbij je hoeken van -180° to +180° moet meten). Zo vind je de volgende twee naastliggende punten. De volgende punten vindt je door deze zelfde zoektocht vanuit de nieuwe twee punten uit te voeren.
Stap 2: Van de nu gevonden punten is het makkelijk om de X- en Y-coordinaten te bepalen onder de rotatie door vermenigvuldigen met de matrix
Je krijgt zo een aantal sinusoiden waarvan je telkens de grootste zou moeten kiezen. Om een algoritme het werk te laten doen moet je bepalen bij welke hoeken de X- resp. Y-waarden van twee opeenvolgende randpunten gelijk zijn. Welnu, dat is natuurlijk precies wanneer de lijn tussen die twee punten verticaal resp. horizontaal staat, en het is niet moeilijk om vanuit de beginsituatie de hoek uit te rekenen waarbij dat gebeurt. Stap 2 in het algoritme is dus het bepalen van de hoeken waarbij er zijden van het convexe omhulsel verticaal danwel horizontaal staan.
Stap 3: Dan komt nu het moment om de doelfunctie in te brengen. Als je bijvoorbeeld niet de oppervlakte maar de omtrek minimaal wilt hebben, dan had je stappen 1 en 2 nog steeds precies hetzelfde kunnen uitvoeren. In stap 3 berekenen we nu de waarde van de doelfunctie (bijvoorbeeld de oppervlakte van de rechthoek) voor de bij stap 2 gevonden 'omslaghoeken'.
Stap 4: Tussen de 'omslagpunten' in worden de uiterste waarden maxX, minX, maxY, minY als functie van de hoek j bepaald door één punt elk en zijn dus gewoon een sinusoide. Van zo'n sinusoide kun je vrij eenvoudig uit te rekenen wanneer de doelfunctie Opp = (maxX - minX) (maxY - minY) (maar eventueel ook bijvoorbeeld Omtrek = 2 (maxX - minX) + 2 (maxY - minY)) minimaal is (werk dit zelf uit via afgeleide nulstellen). In stap 4 moet je dus voor elk interval van hoeken tussen twee in stap 2 bepaalde 'omslaghoeken' uitrekenen wat de minimale waarde van de doelfunctie is (let erop dat het zou kunnen voorkomen dat de gevonden minimaliserende hoek niet in het goede interval zou kunnen liggen).
Stap 5: Tenslotte vergelijk je alle gevonden waarden van de doelfunctie, in de omslaghoeken (stap 3) en in de intervallen tussen de omslagpunten (stap 4). De kleinste waarde die je vindt is de goede.
Merk op dat deze procedure in feite niets anders is dan wat je op de middelbare school leert bij lineair programmeren, maar dan niet lineair, zodat het iets ingewikkelder wordt...
Succes ermee en vraag maar verder als er zaken niet duidelijk zijn, ik hoop dat je er wat aan hebt,
Guido Terra
gt
29-10-2004
#29021 - Vlakkemeetkunde - Student hbo
