WisFaq!

Arcsin funties

Hoe verklaar ik dat bij een bepaalde integraal f:=exp(x)*(1+exp(x))/(sqrt(1-exp(2*x))); met de grenzen van -ln(9) tot -ln(3) ik met verschillende subtituties toch tot verschillende antwoorden kom. Als ik kies voor de substitutie e^x krijg ik als antwoord: arcsin(1/3)-2/3*sqrt(2)-arcsin(1/9)+4/9*sqrt(5) en als ik kies voor de substitutie (sqrt(1-exp(2*x))) krijg ik als antwoord: 4/9*sqrt(5)+arcsin(4/9*sqrt(5))-2/3*sqrt(2)-arcsin(2/3*sqrt(2)). Ik kan niet ontdekken waar nu het verschil tussen beide antwoorden zit. Is het soms een (driehoek verhoudingsverschil? Kunt u mij helpen?

Mark van Weeren
8-9-2004

Antwoord

dag Mark,

Beide antwoorden zijn gelijk.
Het valt nog niet mee om dat aan te tonen, Maple lukt dat niet direct (is(a=b) geeft FAIL), maar je kunt hem wel een handje helpen.
Het komt neer op het aantonen dat
arcsin(4/9*sqrt(5))-arcsin(2/3*sqrt(2))=arcsin(1/3)-arcsin(1/9)
Als je Maple van beide leden de sinus laat uitwerken, komt hij er wel uit, en blijken beide leden inderdaad aan elkaar gelijk te zijn.
Naschrift:
na enig nadenken kan het ook heel goed zonder Maple:

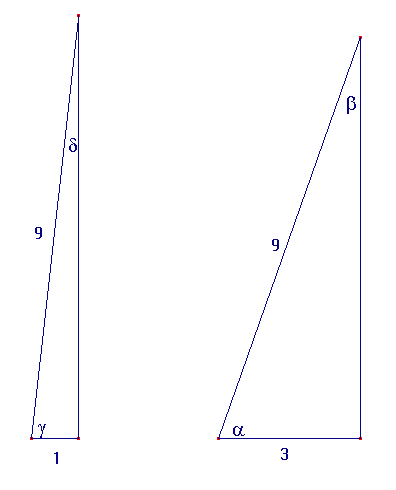
In deze figuur is
a = arcsin(2/3·Ö2)
b = arcsin(1/3)
g = arcsin(4/9·Ö5)
d = arcsin(1/9)
Het zal nu duidelijk zijn dat a + b = g + d

groet,

Anneke
8-9-2004