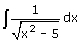
Het zou nochtans moeten te doen zijn aan de hand van de basis integralen.
Jo
4-6-2004
Ik snap niet goed hoe je deze integraal kan oplossen:
Het zou nochtans moeten te doen zijn aan de hand van de basis integralen.Jo
4-6-2004
Neem de substitutie:
t=÷(x2-5)+x, dan
dt=(x/÷(x2-5)+1)dx
dt=(x+÷(x2-5))/÷(x2-5)dx
dus dt=t/÷(x2-5)dx
We krijgen nu dus Ú1/t dt=ln(t)
De primitieve is dus ln(÷(x2-5)+x)
hk
4-6-2004
#24981 - Integreren - Student Hoger Onderwijs BelgiŽ