WisFaq!

Poissonverdeling en exacte waarde berekening

Stel dat je met je vriend de weddenschap afsluit dat van de eerstvolgende vijftien auto's die langskomen tenminste twee auto's nummerborden met twee gelijke eindcijfers hebben. Wat is de kans dat je wint? Bereken zowel de exacte waarde van de kans als de Poisson benaderingswaarde.

BRON: Poisson, de Pruisen en de Lotto (opgave 4.2)

Fred
24-5-2004

Antwoord

Dit is een voorbeeld van een verjaardagsprobleem. Zie eventueel Verjaardagen voor een voorbeeld.

In dit geval gaat het dan om de volgende kans:

P(minstens twee dezelfde)=1 - P(allemaal verschillend)



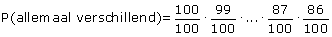
Of in een aangepaste notatie:



P(minstens twee dezelfde)=0,6687

Voor het tweede deel van je vraag kun je het beste kijken op bladzijde 28 en 29 van je Zebraboekje 'Poisson, de Pruisen en de Lotto'. In de tekst staat dat voor de Poissonbenadering 'enige creativiteit' nodig is. Leuk wel!

In dit geval neem je $\lambda$=¹/₂m(m-1)/100 met (in dit geval) m=15.

$\lambda$=1,05.

Met behulp van je GR, een tabel of onderstaand scriptje kan de kans P(X$\geq$1) benaderen:

Met een benadering van 0,6501 zitten we er niet eens erg ver naast...

WvR
29-5-2004