WisFaq!

Oplossing van vergelijking met cosinus hyperbolicus

Graag had ik een oplossing of een tip gekregen om de volgende vergelijking op te lossen naar C₁.

h=^T/_q.Cosh(^q.L/_T+C₁)-^T/_q.Cosh(C₁)

De oplossing zou moeten zijn: C=BgSinh[q.h/(2T.Sinh(n))]-n
En daarbij is: n=q.L/(2.T)

Bij voorbaat dank,

Van den Broeck Joël

Van den Broeck Joel
8-1-2004

Antwoord

In essentie komt de vergelijking neer op:
cosh(x+iets) - cosh(x) = ietsanders,
waaruit x opgelost moet worden.
Laten we eens kijken wat er gebeurt als je een cosh aftrekt van een verschoven cosh.
bijvoorbeeld: cosh(x+1) - cosh(x)

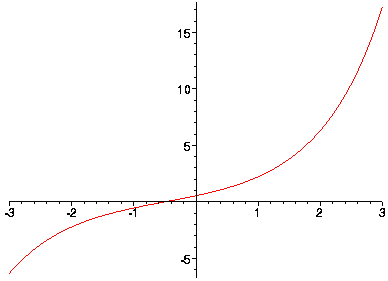
Dit lijkt een sinh met een verschuiving van ¹/₂.
Dit brengt me op een idee.
In verband met het vervolg schrijf ik de oorspronkelijke vergelijking als:
cosh(x+2a) - cosh(x) = b
Nu kun je als volgt het linkerlid herschrijven:
Vervang x+a door y.
Dan krijg je:
cosh(y+a) - cosh(y-a) = b
Dan de definitie van cosh toepassen:

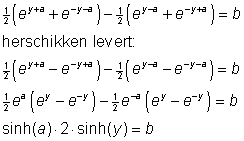
en dit is oplosbaar voor y, en daarmee ben je ook zo bij x.
graag gedaan.
groet,

Anneke
9-1-2004