WisFaq!

Determinanten

ik heb dit proberen oplossen maar zat telkens vast, zou niet weten hoe je dit moet oplossen

Ontbind de determinant van volgende matrix in factoren
[a - b - c 2 a 2 a ]
[ ]
[ 2 b b - c - a 2 b ]
[ ]
[ 2 c 2 c c - a - b]

Manu
6-1-2004

Antwoord

Als je een determinant moet ontbinden komt het erop aan om zoveel mogelijk nullen te krijgen in je determinant.

Hoe kan je nullen 'maken' in je determinant?
Door rij- en kolombewerkingen toe te passen nl.
1) rijen of kolommen wisselen van plaats,
2) bij een rij (resp. kolom) een veelvoud van een andere rij (resp. kolom) optellen
3) een rij of kolom vermenigvuldigen met een getal (verschillend van nul)

Enkel de tweede bewerking laat je determinant onveranderd. Je kan dus ongestraft bij een rij een veelvoud van een andere rij optellen of bij een kolom een veelvoud van een andere kolom.
Als je twee rijen of twee kolommen wisselt van plaats, dan verandert de determinant van teken, en dus opdat je het goede resultaat zou krijgen moet je ook vermenigvuldigen met -1. (Dan heb je m.a.w. 2keer vermenigvuldigd met -1 of dus met 1)
Als je een rij of kolom vermenigvuldigt met een getal (¹0) dan wordt de determinant met datzelfde getal vermenigvuldigd. In dit geval moet je compenseren door opnieuw te vermenigvuldigen met dat getal.
Als het ware zet je gewoon de factor uit een rij of kolom voor de determinant.

Door toepassing van deze bewerkingen tracht je een rij of kolom te maken met één van nul verschillend element en voor de rest nullen.
Zodat je met behulp van de Laplace expansie de orde van de determinant kan reduceren door de determinant te ontwikkelen naar de rij of kolom met de nullen.

Zo ga je verder tot wanneer je eindigt met de determinant van een 1´1 of 2´2 matrix.

Je voorbeeld.
Na de stap staat telkens vermeld welke bewerking gebeurd is.


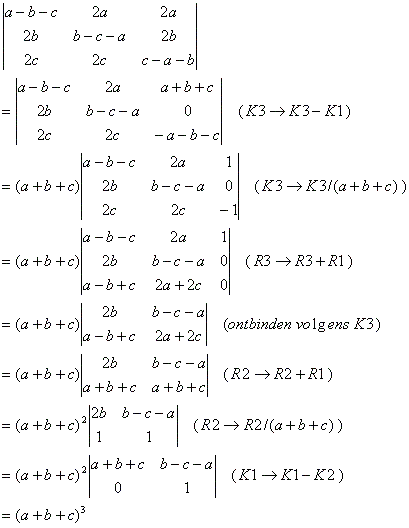
Mvg,

Els
6-1-2004