WisFaq!

Schaatsronding meten

Vraag: Ik wil met een meetklokje op de onderkant van de schaats de ronding meten (bv 20 of 22 meter).
Hierbij zou ik dan een formule moeten hebben, waarbij ik dan over bv 10 cm in het midden de uitslag van het klokje meet, waaruit dan de radius van de denkbeeldige cirkel is te berekenen.

Ik zoek eigenlijk een formule voor een cirkelsegment waarvan de koorde bekend is (10cm) en de hoogte van het cirkelsegment op de helft van de koorde is ook bekend (Dit meet ik met een meetklokje/ micrometer).

Uit deze formule moet dan de straal volgen van de cirkel: dit is dan tevens de ronding van de schaats.

hopelijk is deze info voldoende

Jan Hallink
3-3-2002

Antwoord

Dit is goed aan te pakken met de stelling van Pythagoras (zie tekening)

De afstand KB (dus de halve koorde) noem ik d
De afstand KL noem ik h

Volgens Pythagoras geldt:
MK²+KB²=MB² m.a.w.
(R-h)² + d² = R² uitgewerkt:
R²-2Rh+h²+d² = R² vereenvoudigd:
-2Rh+h²+d²=0 of te wel
2Rh = h²+d² dus

R = (h²+d²)/(2h)

Bij een koorde van 10 cm en een afstand van 0,1 mm geeft dat een straal van 25,0001/0,02 1250 cm (dus 12,5 m)
In feite is het effect van h² erg klein dus als benadering kan genomen worden:
Rd²/(2h)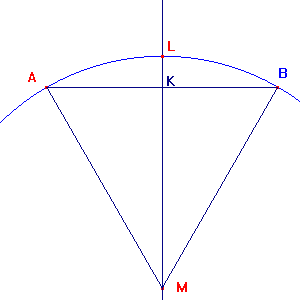

gk
10-3-2002