WisFaq!

Taylorreeks

Hallo,
kunnen jullie me op weg helpen om volgende oef. op te lossen?

Ontwikkel y=sin(2x+3) in een taylorreeks rond p/4 dr gebruik te maken van de cosinus mc laurinreeks
Vervolgens door gebruik te maken van en de cosinus- en de sinus mc laurinreeks.

De Ridder Misja
3-1-2004

Antwoord

Een taylorontwikkeling van f(x) in x=a gaat als volgt:
f(x)=
f(a) + f⁽¹⁾(a)·(x-a)/1! + f⁽²⁾(x-a)²/2! + f⁽³⁾(x-a)³/3! +HOT(4)

Waarbij:
f⁽ⁱ⁾(a) de i-de orde afgeleide is geëvalueerd in het punt a. (verondersteld dat de functie voldoende malen afleidbaar is)
n! = n·(n-1)· ... ·2·1
HOT(t) = hogere orde termen vanaf de t-de macht.

Anders geschreven:
f(x)=

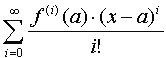
De nulde afgeleide is gewoon de functie zelf, en 0!=1.

Nu kan je dat toepassen op jouw functie. Dus in jouw geval is
f(x)=sin(2x+3)
en a=p/4

Ik heb nu enkel gebruik gemaakt van de ontwikkeling van de sinus in het punt p/4
Als je perse de MacLaurin ontwikkeling van consinus moet gebruiken...kan je misschien de sinus van de som uitschrijven met de somformule

sin(a+b)=sin(a)cos(b)+cos(a)sin(b)

Maar dat lijkt me nogal omslachtig. Het kan dus eenvoudiger op de hoger beschreven manier.

Een MacLaurinontwikkeling is trouwens hetzelfde als een Taylorontwikkeling, maar dan rond het punt x=0.

Koen

km
5-1-2004