WisFaq!

Koordenvierhoek

Als een koordenvierhoektwee even lange diagonalen heeft dan is het een gelijkbenig trapezium. Hoe kan ik dat bewijzen?

Eva
26-5-2003

Antwoord

We gebruiken de stelling:
Gelijke koorden van een cirkel (hier AC=BD) onderspannen gelijke bogen.

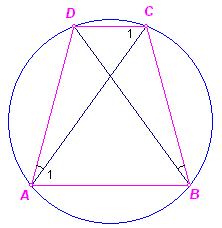
Zodat: bg(ADC) = bg(BCD)
Maar deze hebben bg(CD) gemeenschappelijk, zodat:
bg(AD) = bg(BC), en dus ook (volgens de omgekeerde van de genoemde stelling):
AD = BC
Maar zeker is dan ook C₁ = A₁ (omtrekshoeken op gelijke bogen)
Dus AB // CD (verwisselende binnenhoeken)
ABCD is dus een gelijkbenig trapezium.

dk
26-5-2003