Magisch vierkant of tovervierkant, een vierkant, dat als een dambord verdeeld is in n2 velden; in die n2 velden zet men de getallen 1, 2,... n2 zodanig, dat zij in de richting van de begrenzende zijden en ook in de diagonalen steeds dezelfde som geven.
Voorbeeld met n = 4. De som is 1/2n(n2 + 1) = 34. Tovervierkanten waren in de Middeleeuwen gebruikelijke onderwerpen der rekenkunstenaars. Men vindt bijgaand m. op de ets Melencolia van Albrecht Dürer.
(Uit: Oosthoeks Encyclopedie (deel 9 blz.540 6dedruk - 1968))
Hieronder zie je een uitvergroting van het magische vierkant uit bovengenoemde ets. Ernaast staat het magisch vierkant nog een keer. Je ziet dat de som van de rijen en de kolommen plus de som van de twee diagonalen allemaal 34 zijn:
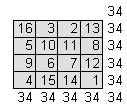
Maar er zitten nog veel meer bijzonderheden in bovenstaand magisch vierkant. Als het vierkant verdeeld in vier vakken, is de som van die vier getallen in zo'n vierkantje ook steeds 34.
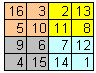
Bij een 4x4 magisch vierkant zijn ook steeds de volgende blauwe vakjes samen 34:
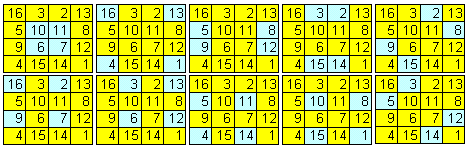
Met behulp van die eigenschappen moet je de volgende magische vierkanten verder in kunnen vullen:
Opdracht 1
Vul onderstaande magische vierkanten verder in:
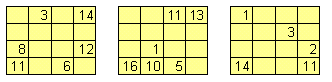
Klik HIER voor een handig excel-werkblad.
Opdracht 2
Misschien dat nu de indruk gewekt wordt dat je dit soort dingen alleen kan doen met de getallen 1 tot en met 16. Niets is minder waar.
Onderzoek of bovenstaande eigenschappen blijven gelden als je
-
bij alle getallen 2 optelt.
-
alle getallen met 2 vermenigvuldigt.
-
van alle getallen het kwadraat neemt.
Algoritme voor oneven vierkanten
Voor oneven magische vierkanten bestaat een eenvoudig algoritme om de getallen op de juiste plaats te krijgen. Neem aan dat we een 3 × 3 vierkant willen maken met de getallen 1 tot en met 9. We beginnen met een 3 × 3 vierkant, waarbij we links, rechts, boven, onder, linksboven, rechtsboven, linksonder en rechtsonder het vierkant nog een keer neer zetten.
Volledig ingevuld zouden we dit plaatje krijgen:
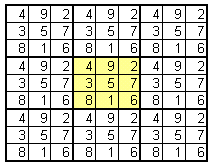
Maar laten we niet op de zaken vooruit lopen. We beginnen met het kleinste getal (1) in het midden onderaan. De plaats van het volgende getal (2) kun je bepalen door twee hokjes omhoog en één hokje naar rechts te gaan, de "paardesprong".
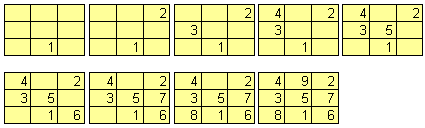
Als een getal in een vakje buiten het vierkant valt, neem je het overeenkomstige vakje in het vierkant. Als je op een vakje terecht komt dat al bezet is kies je het vakje direct boven het vakje waar je vandaan kwam.
(Op de plek waar 4 zou moeten komen staat al 1.)
Zo ga je door tot het hele vierkant gevuld is. Uiteindelijk raakt het hele vierkant gevuld. Je bent klaar zodra je het laatste getal hebt ingevuld. Dit algoritme werkt voor alle oneven vierkanten. Helaas levert dit algoritme niet alle mogelijke magische vierkanten op. Gelukkig zijn er andere manieren om te controleren of een vierkant magisch is.
Opdracht 3
Gebruik bovenstaand algoritme om een magisch vierkant te maken van 5 × 5 met de getallen 1 tot en met 25. Maak ook een magisch vierkant van 7 × 7 m.b.v. het algoritme.
Klik HIER voor een handig excel-werkblad.
Eigenschappen van vierkanten van 5 × 5
Voor het oplossen van gewone magische vierkanten van 5 × 5 is het nuttig te weten dat:
-
het middelste getal altijd het middelste getal van alle voorkomende getallen is
-
de tegenover elkaar liggende hoekgetallen samen steeds het dubbele van het middelste getal vormen.
In het voorbeeld hieronder kun je zien hoe dat werkt. Twee dezelfde gekleurde vakjes zijn samen steeds evengroot als twee keer het donker blauwe vakje.
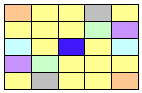
Je kunt dit controleren bij je oplossing van opdracht 3.
Opdracht 4
Gebruik bovengenoemde eigenschappen om de volgende magische vierkanten op te lossen. Er onder staat steeds wat de som van de rijen en kolommen is.
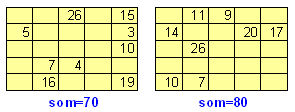
Klik HIER voor een handig excel-werkblad.
Mogelijke startpunten
