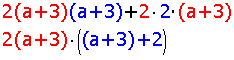Ik kwam 'ergens' een hele verzameling opgaven tegen over ontbinden in factoren. Op deze pagina zal ik die 's bespreken.
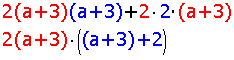
Bij (a+1)^2+(a+1) kun je de gemeenschappelijk factor (a+1) buiten haakjes halen. Je moet dan goed kijken wat er tussen de haakjes komt te staan:
-
(a+1)^2+(a+1)=
(a+1)((a+1)+1)=
(a+1)(a+2)
Idem voor 2(a+3)^2+4(a+3):
-
2(a+3)^2+4(a+3)=
2(a+3)((a+3)+2)=
2(a+3)(a+5)
Nog maar een voorbeeld: (a+3)^2·(b+1)-2(a+3)(b+1). Je kunt hier de gemeenschappelijke factor (a+3)(b+1) buiten haakjes halen.
-
(a+3)^2·(b+1)-2(a+3)(b+1)=
(a+3)(b+1)((a+3)-2)=
(a+1)(a+3)(b+1)
Kijken naar (a+1)^2·(a+2)-(a-1)·(a+2)^2. Je kunt alleen de factor (a+2) buiten haakjes halen.
-
(a+1)^2·(a+2)-(a-1)·(a+2)^2=
(a+2)((a+1)2-(a-1)(a+2)=
(a+2)(a^2+2a+1-(a^2+a-2))=
(a+2)(a^2+2a+1-a^2-a+2)=
(a+2)(a+3)
Of zo:
-
3·(a + 2)^2·(a - 2) + 9·(a + 2)·(a - 2)^2=
3(a+2)(a-2)((a+2)+3(a-2))=
3(a+2)(a-2)(a+2+3a-6)=
3(a+2)(a-2)(4a-4)=
12(a+2)(a-2)(a-1)
En...
-
-2(a+4)^3+8(a+4)^2(a+2)=
2(a+4)^2(-(a+4)+4(a+2))=
2(a+4)^2(-a-4+4a+8)=
2(a+4)^2(3a+4)
F.A.Q.
Extra