Als je aan de waarde van een toevalsvariabele (ook wel stochast genoemd) kansen toekent spreekt men van een kansverdeling.
Een toevalsvariabele is een variabele waarvan de waarde een numerieke uitkomst is van een toevalsverschijnsel.
Voorbeeld
Je gooit met 8 munten. Het aantal kop per worp noem je X.
X is dan de toevalsvariabele.
Omdat de toevalsvariabele weinig waarden aanneemt, zou je de kansverdeling in een tabel kunnen zetten.
|
x |
0 |
1
|
2 |
3 |
4 |
|
P(X = x) |
0,004 |
0,031 |
0,109 |
0,219 |
0,273 |
|
x |
5 |
6 |
7 |
8 |
|
P(X=x) |
0,219 |
0,109 |
0,031 |
0,004 |
Maar je kunt zo'n kansverdeling ook met een grafiek weergeven:
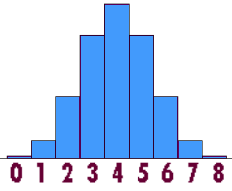
Hierboven staat een voorbeeld van een kansverdeling van een discrete toevalsvariabel. Het is een voorbeeld van een binomiale kansverdeling.
Voorbeeld
Je gooit met 4 dobbelstenen. Geef de kansverdeling van het aantal zessen dat je gooit met één worp.
Ook dit is een voorbeeld van een binomiale kansverdeling.
Je kunt met 4 dobbelstenen 0, 1, 2, 3 of 4 zessen gooien.
Eerst maar eens de kansen uitrekenen.
|
Aantal zessen
|
0
|
1
|
2
|
3
|
4
|
|
P
|
.482
|
.386
|
.116
|
.015
|
.001
|
Of in een grafiek:
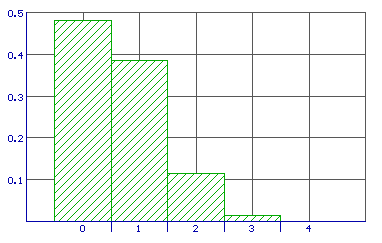
Naast discrete toevalsvariabelen bestaan er ook kansverdelingen met een continue toevalsvariabele. De normale verdeling is daar een voorbeeld van.
F.A.Q.







