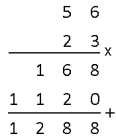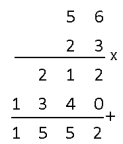In het decimale stelsel heb je op school ooit de tafels van vermenigvuldigen geleerd. Dat was nodig om bijvoorbeeld snel en effcient te kunnen vermenigvuldigen. Dat is dan weer handig als je een een staartdeling wilt kunnen maken.
Vermenigvuldigen in het decimale stelsel
We kijken naar $23\cdot56$. Je kunt dat zo uitrekenen:
- $23\cdot56=20\cdot56+3\cdot56=1120+168=1288$
Je kunt ook de getallen 'onder elkaar zetten':
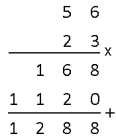
Als je goed kijkt dan zie je dat dat eigenlijk hetzelfde is.
Vermenigvuldigen in het achttallig stelsel
In het achttallig stelsel kan je ook vermenigvuldigen.:
- $23\cdot56=20\cdot56+3\cdot56=1340+212=1552$
Je kunt ook bij het achttallig stelsel de getallen 'onder elkaar zetten'. Je krijgt dan:
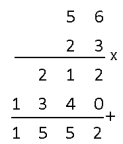
Maar misschien merk je wel dat dit niet zo maar vanzelf gaat. Eigenlijk moet je opnieuw de tafels van vermenigvuldigen leren voor het achttallig stelsel. Dat gaan we maar niet doen. Hier zie je daarvan een overzicht...

Als je dus $3\cdot56$ wilt bereken dan kijk je bij $3\cdot50=170$ en $3\cdot6=22$. Dat is dan samen $212$. Pfff..:-)