Von Koch-krommen
Een fractal is een meetkundige figuur waarin een zelfde motief zich steeds op kleinere schaal herhaalt. Een voorbeeld van zo'n figuur is de zogenaamde Von Koch-kromme. Je begint bijvoorbeeld met een lijnstukje

maar in plaats van het lijnstukje te tekenen teken je 4 andere lijnstukjes.
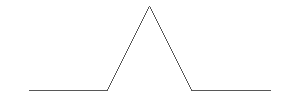
Deze lijnstukjes teken je ook niet. In plaats daarvan teken je voor elk van deze 4 lijnstukjes weer 4 lijnstukjes. Zodat de figuur bestaat uit 16 lijnstukjes:

Maar deze 16 lijnstukjes teken je ook niet. Voor elk lijnstukje teken je weer 4 lijnstukjes:

Maar, je snapt het al, ook deze lijnstukjes tekenen we niet. In plaats daarvan tekenen we weer voor elk lijnstukje de 4 lijnstukjes. Zodat je deze figuur krijgt:

En zo zou je nog een tijdje door kunnen gaan.
De denkbeeldige kromme die je krijgt als je hier oneindig lang mee doorgaat is wel heel bijzonder. Bij elke stap wordt de lengte van de kromme groter. Sterker nog: elk onderdeeltje van de kromme, hoe klein ook, heeft een oneindige lengte.
Meer dan alleen mooie plaatjes...
Experimenten met fractals leveren hele mooie plaatjes op. Hieronder zie je daar enkele voorbeelden van:








Deze plaatjes zijn gemaakt met het programma freeware-programma Fractint. Ondanks dat deze plaatjes met de computer gemaakt zijn kun je vaak bekende patronen en structuren ontdekken. Hieronder zie je voorbeelden van plaatjes uit de natuur:

Je ziet hier bijvoorbeeld zaken als:
- Elektrische ontlading
- Een termietencolonie
- Bacterie-groei
- Rotsformaties
- Neuronen
- Bliksem
- Embryo
- Kristal
- Retina
- Bladeren
Fractals hebben te maken met Chaos-theorie:
"De onregelmatige kant van de natuur, de discontinue en grillige kant, dat waren raadsels voor de natuurwetenschap. In de jaren zeventig begonnen een paar wetenschappers in de Verenigde Staten en Europa een weg te vinden in de wanorde. Het waren wis- en natuurkundigen, biologen en scheikundigen, die allemaal op zoek waren naar een verband tussen verschillende soorten onregelmatigheid. Tien jaar later is "chaos" de korte roepnaam geworden voor de snelgroeiende beweging die de structuur van de gevestigde wetenschap hervormt. Het wemelt van de conferenties en tijdschriften over chaos."
(Chaos De derde wetenschappelijke revolutie
James Gleick, 1987, pag. 11 en 14) |
Opdracht
Schrijf een werkstuk waarin minimaal de volgende zaken besproken worden:
- De oorsprong van de naam 'fractals'.
- Wie is Mandelbroth?
- Wat zijn complexe getallen en wat hebben ze met fractals te maken?
- Wat is fractal-muziek?
- Wat is "chaos"?
- Voorbeelden van mooie fractals.
Afsluiting
Naast het inleveren van een werkstuk zal dit onderwerp worden afgesloten door een computerpresentatie en het organiseren van een computerpracticum voor de hele klas. Dit laatste kan een internetopdracht zijn, maar mag ook het werken met een computerprogramma zijn. Je kunt hierbij denken aan een grafisch programma, maar een muziekprogramma mag ook.
Verwijzingen





















