Als je k elementen kiest uit een verzameling van n elementen, waarbij ieder element meerdere keren gekozen mag worden en waarbij niet gelet wordt op de volgorde dan heb je te maken met een herhalingscombinatie.
Het aantal herhalingscombinaties kan worden berekend met de volgende formule:
$aantal=\pmatrix{n-1+k\\k}$
Voorbeeld
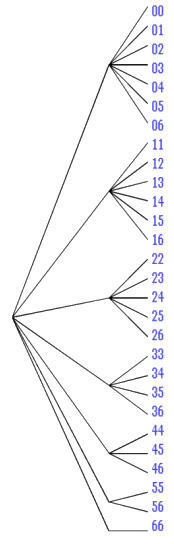
Op een dominosteen stelt het aantal ogen op iedere helft van een steen een getal voor. De getallen kunnen 0,1,2,3,4,5 of 6 zijn. Alle mogelijke verschillende stenen komen in het spel voor.
Hoeveel verschillende dominostenen zijn er?
Antwoord:
$aantal=\pmatrix{7-1+2\\2}=\pmatrix{8\\2}=28$
of....
7 + 6 + 5 + 4 + 3 + 2 + 1 = 28
Voorbeeld
Een onderwijzer moet 3 potloden, 2 linialen, 7 vulpennen verdelen in een klas van 12 leerlingen.
-
Op hoeveel manieren kan dit gebeuren als niet elke leerling noodzakelijk een voorwerp krijgt, maar wel alles uitgedeeld wordt?
-
Op hoeveel manieren kan dit gebeuren als niet elke leerling noodzakelijk een voorwerp krijgt en niet alle voorwerpen noodzakelijk uitgedeeld worden?
Uitwerking
Je kunt het verdelen van de 3 potloden over 12 leerlingen (zoals dat hier gebeurt) opvatten als herhalingscombinatie. Dit kan dan op '14 boven 3' manieren. Zo ook voor 2 linealen ('13 boven 2') en de 7 linialen ('18 boven 7').
Bij vraag 2 doe je dat ook, alleen neem je er een 13e leerling bij (de niet uitgedeelde items). Verder als bij a.
a. $\pmatrix{14\\3}\pmatrix{13\\2}\pmatrix{18\\7}=903.547.008$
b. $\pmatrix{15\\3}\pmatrix{14\\2}\pmatrix{19\\7}=2.086.315.140$
F.A.Q.
