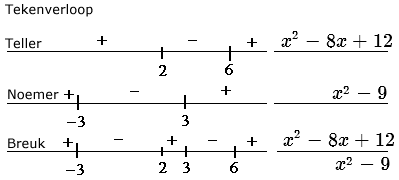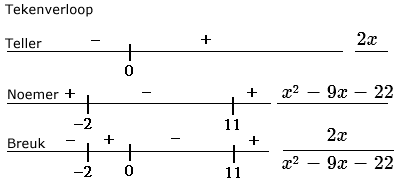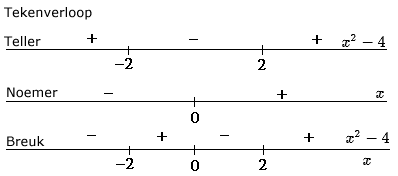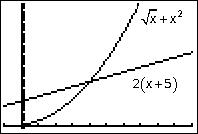Opgave 1
\eqalign{ & a. \cr & 3x + 4 < 9x - 14 \cr & - 6x < - 18 \cr & x > 3 \cr & \cr & b. \cr & - \frac{1} {3}x - 14 \ge 7 \cr & - \frac{1} {3}x \ge 21 \cr & x \le - 63 \cr & \cr & c. \cr & 2(4 - x) \le 9(x + 2) \cr & 8 - 2x \le 9x + 18 \cr & - 11x \le 10 \cr & x \ge - \frac{{10}} {{11}} \cr}
Opgave 2
a.
Los op: \eqalign{\frac{x^{2}-8x+12}{x^{2}-9}\ge0}
De teller is nul bij x=2 en x=6.
De noemer is nul bij x=-3 en x=3.
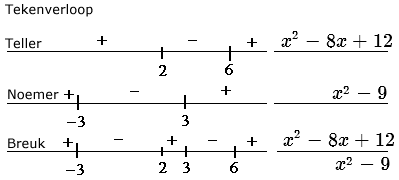
Oplossing: x\lt-3\vee2\le x\lt3\vee x\ge6
b.
Los op: \eqalign{\frac{2x}{x^{2}-9x-22}\ge0}
De teller is nul bij x=0 en de noemer is nul bij x=-2 en x=9.
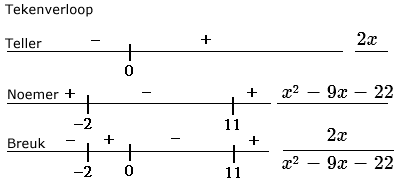
Oplossing: -2\lt x\le0\vee x\gt11
c.
\eqalign{ & x < \frac{4} {x} \cr & x - \frac{4} {x} < 0 \cr & x \cdot \frac{x} {x} - \frac{4} {x} < 0 \cr & \frac{{x^2 }} {x} - \frac{4} {x} < 0 \cr & \frac{{x^2 - 4}} {x} < 0 \cr}
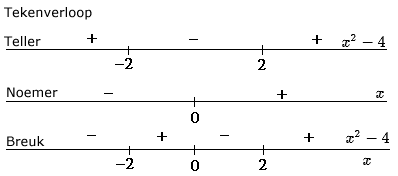
Oplossing: x\lt-2\vee 0\lt x\lt2
Opgave 3
\eqalign{ & \frac{{x^2 - 4x + 2}} {{x - 1}} \le x + 2 \cr & \frac{{x^2 - 4x + 2}} {{x - 1}} - (x + 2) \le 0 \cr & \frac{{x^2 - 4x + 2}} {{x - 1}} - \frac{{\left( {x + 2} \right)\left( {x - 1} \right)}} {{x - 1}} \le 0 \cr & \frac{{x^2 - 4x + 2}} {{x - 1}} - \frac{{x^2 + x - 2}} {{x - 1}} \le 0 \cr & \frac{{ - 5x + 4}} {{x - 1}} \le 0 \cr & x \le \frac{4} {5} \vee x > 1 \cr}
Opgave 4
\eqalign{ & \sqrt x + x^2 \le 2\left( {x + 5} \right) \cr & Y1 = \sqrt x + x^2 \cr & Y2 = 2\left( {x + 5} \right) \cr}
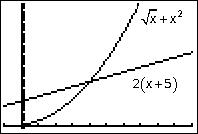
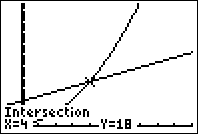
Het snijpunt is (4,18). Y1 heeft als 'startpunt' (0,0).
Oplossing: 0\le x\le 4