©2012 WisFaq

1. Inleiding telproblemen

Handig tellen vereist een systematische aanpak. Door problemen met elkaar te vergelijken stuit je vaak op allerlei overeenkomsten en regelmatigheden. De kunst is vaak die regelmaat te ontdekken.

Machtsbomen

Eén manier om handig te kunnen tellen is een boomdiagram.

Je gooit 3 keer met een munt (kop of munt). Hoeveel verschillende uitkomsten zijn er ?

De eerste keer kun je kop of munt gooien, de tweede keer ook en de derde keer ook, dus zijn er 8 mogelijkheden:
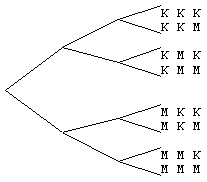Dit kun je aangeven met een boomdiagram, hierbij is naar boven 'kop' en naar beneden 'munt'. Uit elk punt van de boom vertrekken evenveel takken. (boomdiagrammen zijn een soort grafen !)

  1. Wat zou het antwoord zijn als je 4 of 5 of zelfs met 6 munten gooit?
    antwoord
  2. En als je met 20 munten gooit hoeveel verschillende worpen zijn er?
    antwoord

Je kunt het aantal mogelijkheden eenvoudig uitrekenen met machten. Bij elke munt neemt het aantal mogelijkheden toe met een macht. Men noemt dit soort boomdiagrammen wel machtsbomen.

Faculteitsbomen

Soms vertrekken er van elk punt niet evenveel takken.

Bij een vereniging worden 3 mensen (A,B en C) in het bestuur gekozen die de functie van voorzitter, penningmeester en secretaris moeten vervullen. Op hoeveel manieren kan men deze 3 functies over deze 3 mensen verdelen ?
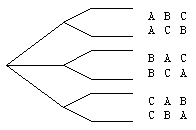Je krijgt nu een ander soort boom. Nu vertrekt er van elk punt steeds een lijn minder.

Je maakt hier de vermenigvuldiging:

3 x 2 x 1 = 6.

Op hoeveel manieren kun je 10 functies over 10 mensen verdelen?

Op dezelfde manier:

10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 3.628.800

Bovenstaand product noemen we 10 faculteit. We gebruiken daarvoor de notatie 10!. Op je rekenmachine zit een toets x! waarmee je faculteiten uit kunt rekenen.

We noemen een boom als hierboven wel faculteitsboom.

Vaak komen we een stukje van een faculteitsboom tegen. Bijvoorbeeld als je wilt weten op hoeveel manieren je 3 functies over 10 mensen wilt verdelen. Dit kan op 10 x 9 x 8 manieren.

Wegendiagrammen

In een wegendiagram worden wegen die naar één punt leiden samengevoegd.



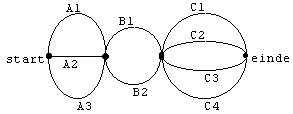
Hierboven staat een voorbeeld van een wegendiagram.

Op hoeveel manieren kun je van START naar EINDE ?

Er zijn in totaal 24 verschillende routes van start naar einde mogelijk.
Dit kun je uitrekenen door 3 x 2 x 4 = 24

Je kunt op 25 manieren van P naar Q en op 11 manieren van Q naar R.

Roosterdiagrammen

Als je bij een telprobleem steeds een keuze gemaakt moet worden uit twee alternatieven, dan ontstaat er een zeer regelmatig wegendiagram. We noemen zo'n wegendiagram een roosterdiagram. Het ziet er uit als roosterpapier.

Voorbeelden van een keuze tussen twee alternatieven:

Een gezin heeft 5 kinderen. Op hoeveel verschillende manieren kan het gezin zijn samengesteld?
Dit kan op 25 = 32 manieren.

Als je niet op de volgorde let, zijn er 6 verschillende samenstellingen mogelijk. Hierbij gebruik je de driehoek van Pascal.



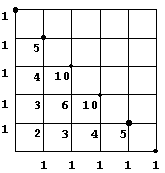
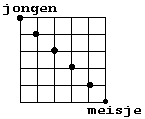
Elk volgend getal kun je uitrekenen door de getallen waar je vandaan kan komt op te tellen. Als je naar rechts gaat is het een meisje en als je naar boven gaat is het een jongen.

Voor een gezin met 4 kinderen met 2 jongens en 2 meisjes zijn er als je wel op de volgorde let, 6 verschillende mogelijkheden.

F.A.Q.

Terug Home