
Algebra
Analyse
Bewijzen
De grafische rekenmachine
Discrete wiskunde
Fundamenten
Meetkunde
Oppervlakte en inhoud
Rekenen
Schoolwiskunde
Statistiek en kansrekenen
Telproblemen
Toegepaste wiskunde
Van alles en nog wat

|
\require{AMSmath}










B. Oefeningen 2
- In een vaas zitten 8 witte, 4 blauwe en 2 rode ballen. We trekken steeds drie ballen uit de vaas zonder terugleggen.
- Bereken de kans op 3 witte ballen.
- Bereken de kans op 2 witte ballen.
- Bereken de kans op 3 verschillend gekleurde ballen.
- Bereken de kans op minstens 2 ballen van dezelfde kleur.
- In een vaas zitten 10 knikkers. 5 blauw, 3 rood en 2 wit. We halen steeds, met terugleggen 3 knikkers uit de vaas.
- Bereken de kans op 1 wit, 1 blauw en 1 rood.
- Bereken de kans op 3 blauwe knikkers.
- Bereken de kans op 3 rode knikkers.
- Bereken de kans op 3 knikkers van dezelfde kleur.
- Bereken de kans op minstens 1 blauwe knikker.
- Hieronder is een tabel gegeven met informatie over de instroom van nieuwe studenten aan een bepaalde hogeschool.

- Wat is de kans dat iemand minstens een havo (E) vooropleiding heeft?
- Wat is de kans dat iemand vwo (F) vooropleiding heeft en deeltijd heeft gekozen?
- Wat is de kans dat iemand volltijd studeert of een havo (E) vooropleiding heeft?
- Wat is de kans dat iemand niet duaal (C) studeert?
- Sluiten de gebeurtenissen havo (E) vooropleiding en duaal studeren elkaar uit?
- Zijn de gebeurtenissen vwo (F) vooropleiding en deeltijd studeren onafhankelijk?
- Een pincode bestaat uit 4 cijfers van 0..9.
- Hoeveel pincodes kan je maken?
- Hoeveel pincodes zijn er die bestaan uit vier verschillende cijfers?
- Hoeveel pincode zijn er waarbij één of meerdere cijfers meerdere keren voorkomen?
- Hoeveel pincodes zijn er waarbij na elkaar dezelfde cijfers voorkomen? (bijv 9336, 4491)
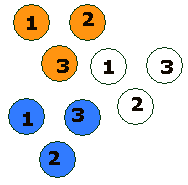 Een vaas bevat negen knikkers: drie rode, drie witte en drie blauwe. Van elke kleur is er op één knikker het cijfer 1 gezet, op één knikker het cijfer 2 en op één knikker het cijfer 3. Laurens haalt aselect een knikker uit de vaas. Een vaas bevat negen knikkers: drie rode, drie witte en drie blauwe. Van elke kleur is er op één knikker het cijfer 1 gezet, op één knikker het cijfer 2 en op één knikker het cijfer 3. Laurens haalt aselect een knikker uit de vaas.
Gebeurtenis A is het trekken van een blauwe knikker.
Gebeurtenis B is het trekken van een knikker met nummer 2.
- Leg met behulp van een berekening uit dat P(A|B) gelijk is aan P(B|A).
- Onderzoek of A en B onafhankelijk zijn.
Laurens legt de getrokken knikker terug in de vaas. Vervolgens haalt hij er zonder te kijken in één greep twee knikkers uit.
- Hoe groot is de kans op twee knikkers van dezelfde kleur?
- Bereken de kans dat de som van de cijfers op de twee getrokken knikkers vier is.
- Hoe groot is de kans op minstens één keer het cijfer 3?
- Daar sta je dan 's avonds laat voor de geldautomaat! Was het 5734 of 5347....? Het enige wat je nog zeker weet is dat je pincode bestaat uit de vier cijfers 3,4,5 en 7 en dat de code begint met 5. Dat wordt proberen........en het pasje wordt geblokkeerd na drie foute pogingen.
- Hoeveel verschillende pincodes zijn er dan mogelijk?
- Bereken bij willekeurig intoetsen van de laatste drie getallen de kans op 2 cijfers op de goede positie.
- Bereken de kans dat het met willekeurig proberen lukt om geld uit de machine te krijgen.
- Je ziet hier de uitslagen van 4 dobbelstenen:
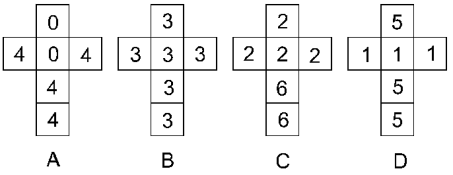
Laat iemand een dobbelsteen uitkiezen en wed vervolgens om een euro dat je hoger zult gooien.
Als je tegenstander A kiest, kies jij D. Kiest hij of zij B, dan kies je A. Mocht je tegenstander C kiezen, dan kies je B. Als hij of zij D kiest, dan kies je C. Geloof het of niet, je zult uiteindelijk vaker winnen, dan je tegenstander!
Laat zien dat 'A' wint van 'B', 'B' van 'C', 'C' van 'D' en 'D' van 'A'.

©2004-2025 WisFaq
|
|

