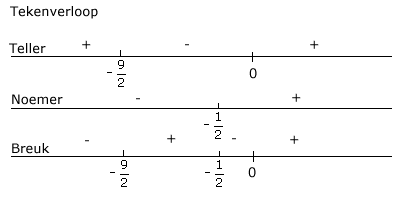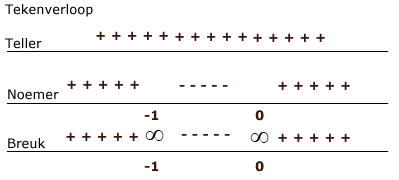Uitwerkingen

Opgave 1

$
\eqalign{
  & \frac{{4 + 2x}}
{{x - 1}} \leq 3  \cr
  & \frac{{4 + 2x}}
{{x - 1}} - 3 \leq 0  \cr
  & \frac{{4 + 2x}}
{{x - 1}} - 3 \cdot \frac{{x - 1}}
{{x - 1}} \leq 0  \cr
  & \frac{{4 + 2x}}
{{x - 1}} - \frac{{3x - 3}}
{{x - 1}} \leq 0  \cr
  & \frac{{4 + 2x - 3x + 3}}
{{x - 1}} \leq 0  \cr
  & \frac{{7 - x}}
{{x - 1}} \leq 0 \cr}
$

De oplossing is x$<$1 of x$\geq$7

Opgave 2

$
\eqalign{
&Stap\,\,1.\cr
&\frac{{-10x+3}}
{{2x+1}}\leq2x+3\cr
&\frac{{-10x+3}}
{{2x+1}}-\left({2x+3}\right)\leq0\cr
&\frac{{-10x+3}}
{{2x+1}}-\frac{{\left({2x+3}\right)\left({2x+1}\right)}}
{{2x+1}}\leq0\cr
&\frac{{-10x+3}}
{{2x+1}}-\frac{{4x^2+8x+3}}
{{2x+1}}\leq0\cr
&\frac{{-10x+3-4x^2-8x-3}}
{{2x+1}}\leq0\cr
&\frac{{-4x^2-18x}}
{{2x+1}}\leq0\cr
&\frac{{4x^2+18x}}
{{2x+1}}\geq0\cr
&Stap\,\,2.\cr
&4x^2+18x=0\Rightarrow2x\left({2x+9}\right)=0\Rightarrow x=0\vee x=-\frac{9}
{2}\cr
&2x+1=0\Rightarrow x=-\frac{1}
{2}\cr}
$

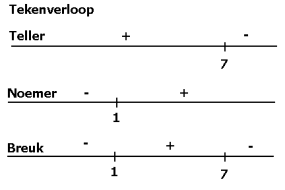
$Stap\,3$

$Stap\,4$

$
\eqalign{
&We\,\,keken\,\,naar\,\,\frac{{4x^2+18x}}
{{2x+1}}\geq0\cr
&{Oplossing}:-\frac{9}
{2}\leq x<-\frac{1}
{2}\vee x\geq0\,\,\,dan\,\,wel:[-\frac{9}
{2},-\frac{1}
{2}>\cup[0,\to>\cr}
$

Opgave 3

Eerst de linkerkant:

$
\eqalign{
  & \frac{{x - 1}}
{{x - 2}} \geq  - 1  \cr
  & \frac{{x - 1}}
{{x - 2}} + 1 \geq 0  \cr
  & \frac{{x - 1}}
{{x - 2}} + \frac{{x - 2}}
{{x - 2}} \geq 0  \cr
  & \frac{{2x - 3}}
{{x - 2}} \geq 0  \cr
  & x \leq 1\frac{1}
{2} \vee x > 2 \cr}
$

Dan de rechterkant:

$
\eqalign{
  & \frac{{x - 1}}
{{x - 2}} \leq 1  \cr
  & \frac{{x - 1}}
{{x - 2}} - 1 \leq 0  \cr
  & \frac{{x - 1}}
{{x - 2}} - \frac{{x - 2}}
{{x - 2}} \leq 0  \cr
  & \frac{1}
{{x - 2}} \leq 0  \cr
  & x - 2 < 0  \cr
  & x < 2 \cr}
$

Dus de uiteindelijke oplossing wordt:

$
\eqalign{
  &  - 1 \leq \frac{{x - 1}}
{{x - 2}} \leq 1  \cr
  & x \leq 1\frac{1}
{2} \cr}
$

Opgave 4

Stap 1.

$
\eqalign{
  & 3 + {2 \over x} \le {1 \over {x + 1}}  \cr
  & 3 + {2 \over x} - {1 \over {x + 1}} \le 0  \cr
  & {{3x\left( {x + 1} \right)} \over {x(x + 1)}} + {{2(x + 1)} \over {x(x + 1)}} - {x \over {x(x + 1)}} \le 0  \cr
  & {{3x^2  + 3x + 2x + 2 - x} \over {x(x + 1)}} \le 0  \cr
  & {{3x^2  + 4x + 2} \over {x(x + 1)}} \le 0 \cr}
$

Stap 2.

$
\eqalign{
  & 3x^2  + 4x + 2 = 0 \Rightarrow {\text{geen}}\,\,\,{\text{oplossing}}  \cr
  & x(x + 1) = 0 \Rightarrow x =  - 1 \vee x = 0 \cr}
$

Stap 3.

Stap 4.

Oplossing: $
 - 1 < x < 0
$

©2004-2024 WisFaq