Antwoorden

Eén

---

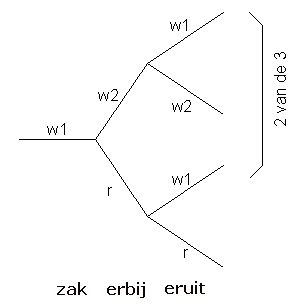
Bij het 'eruit' halen van de bal zijn er 4 mogelijkheden. Je hebt er een witte bijgedaan, je pakt er een witte uit (dat kan op twee manieren: w1 of w2) of je hebt er een rode bijgedaan en je pakt er een witte (w2) of een rode (r) uit.

De kans op elk van deze 4 gebeurtenissen is even groot. Je weet al dat je er een witte uitpakt. Bij 2 van de 3 mogelijkheden is de andere bal ook wit.

De kans is ²/₃.

Of:

Kijk naar de gebeurtenissen A en B:

1. 1^e wit
2. 2^e wit

Er geldt: $
P\left( {A|B} \right) = \frac{{P(A\,\,en\,\,B)}}
{{P(B)}}
$

P(B)=³/₄
P(A en B)=¹/₂

$
P\left( {A|B} \right) = \Large \frac{{\,\,\frac{1}
{2}\,\,}}
{{\frac{3}
{4}}} = \frac{2}
{3}
$

Twee

---

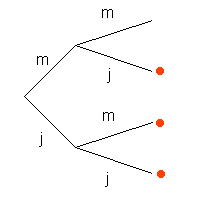
De drie gebeurtenissen MJ, JM en JJ zijn even waarschijnlijk. De kans dat het tweede kind een meisje is is ²/₃.

Drie

---

Bij 'lastige' problemen of als je 't even niet ziet kan je altijd een boomdiagram tekenen of een deel ervan!

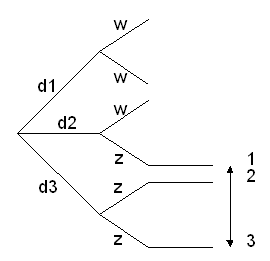
Hiernaast zie je in het boomdiagram dat er drie mogelijkheden met uitkomst 'bovenkant is rood' zijn.

P(1,Rood)=¹/₆
P(1,Rood)=¹/₆
P(3,Rood)=¹/₆

Bij 2 van deze 3 mogelijkheden is de achterkant ook rood, bij 1 niet.
De kans dat de achterkant rood is dus ²/₃.

Vier

---

Bij 2 van de 3 mogelijkheden zit er nog een zwarte bal in de doos de kans is dus ²/₃

Of:

$
\eqalign{
& Er\,\,geldt:\,\,P\left( {A|B} \right) = \frac{{P(A\,\,en\,\,B)}}
{{P(B)}} \cr
& P(pak\,\,zwart\,\,|\,\,zwart\,\,blijft\,\,over) = \frac{{P(pak\,\,zwart\,\,EN\,\,zwart\,\,blijft\,\,over)}}
{{P(zwart\,\,blijft\,\,over)}} = \frac{{\,\,\frac{1}
{3}\,\,}}
{{\frac{1}
{2}}} = \frac{2}
{3} \cr}
$

©2004-2024 WisFaq