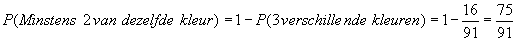Alternatieve aanpak opgave 1
1.
- De kans op 3 witte ballen kun je uitrekenen door het 'experiment' gewoon even na te lopen: Wat is de kans dat de eerste bal wit is? Er zijn 8 witte van 14 dus 8/14.
Wat is de kans dat de tweede bal wit is? Er zijn nog 13 ballen over waarvan er 7 wit zijn.
De kans op een witte is 7/13.
Wat is de kans dat de derde ook wit is? Er zijn 6 wit van de 12 dus 6/12.
De kans op 3 witte ballen is 8/14·7/13·6/12 = 336/2184 = 2/13.- Er zijn eigenlijk twee soorten ballen: witte en niet-witte. Wat is nu de kans op (precies) twee witte ballen? Er zijn nu verschillende mogelijkheden: de eerste 2 ballen kunnen wit zijn en de derde niet, de eerste en de derde kunnen wit zijn, enzovoort....
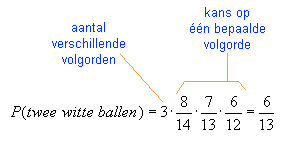
Om de kans uit te rekenen kun je kijken naar één zo'n volgorde. We nemen maar wit, wit, niet-wit. We kijken naar P(w,w,n), dus de kans op precies die volgorde!P(w,w,n) = 8/14·7/13·6/12 = 2/13
Vervolgens kijk je hoeveel verschillende volgordes je kunt maken met twee witte en een niet-witte. Dit kan op 3 verschillende manieren, dus de kans op precies twee witte ballen is 3·2/13 = 6/13
Dit is een patroon dat je vaak zult tegenkomen:
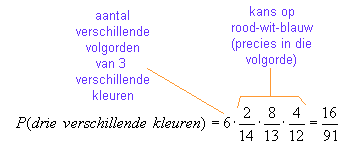
- Ook hier kun je deze methode handig gebruiken:
- De laatste vraag valt in de categorie "een beetje flauw", want als je niet 3 verschillende ballen hebt, heb je te maken met minstens 2 dezelfde. Anders gezegd:



©2004-2025 WisFaq