WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

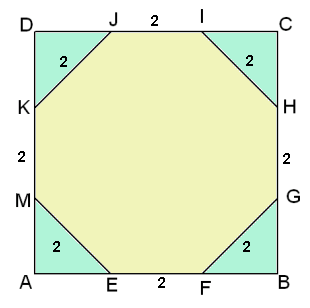
Ruimtemeetkunde

Afgeknotte kubus

Door van een kubus de hoeken af te snijden, verkrijgt men het ruimtelichaam zoals in de figuur. Het wordt begrensd door zes regelmatige achthoeken en acht gelijkzijdige driehoeken waarvan alle zijden gelijk zijn aan 1. Wat is het volume van dat lichaam? Volgens mij moet je eerst a zoeken,nl. de ribbe van de oorspronkelijke kubus en dit zou 1+sqrt2 moeten zijn, maar ik snap niet hoe je hieraan komt.
Mona
26-1-2025

Antwoord

Misschien heb je iets aan Afgeknotte hexaëder met zijden van twee?
Helpt dat? Anders nog maar even verder vragen.
WvR
26-1-2025

Re: Afgeknotte kubus

Niet helemaal, ik snap echt niet dat de zijde van de kubus 1+sqrt(2) is als je weet dat van de afgeknotte kubus er achthoeken ontstaan en driehoeken met zijde 1
Mona
26-1-2025

Antwoord

Neem aan dat HI=2. Bereken HC met de stelling van Pythagoras. Je weet HG=2 zodat de lengte van BC gelijk is aan $2\sqrt{2}$ +2.

Je kunt nu zelf hetzelfde doen voor HI=1. Dat moet nu wel lukken…

Naschrift
Het antwoord op de vraag over tetraëder staat op
De oppervlakte en inhoud van een tetraëder

WvR
26-1-2025