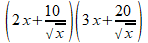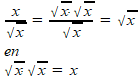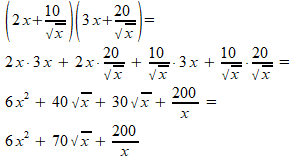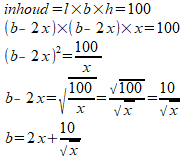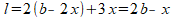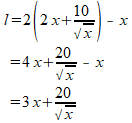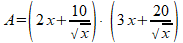WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Formules

Dozen met vaste inhoud

Zou u de derde bulletpoint bij het 1e voorbeeld/de tweede bulletpoint bij het 2e voorbeeld willen uitleggen? Van dit eindexamen:
vwo wiskunde B examen 2008 b1 tweede tijdvak
Dankuwel.
A
13-2-2024

Antwoord

Ik begrijp dat het gaat om het wegwerken van de haakjes in:

Bedenk dan eerst dat geldt:

Dit passen we toe bij het wegwerken van de haakjes:

Is hiermee het probleem opgelost? Zo nee, stel dan gerust een vervolgvraag, geef dan aan waar het probleem precies ligt.
GHvD
13-2-2024

Re: Dozen met vaste inhoud

Dankuwel, dit is nu duidelijker. Zou u mij willen uitleggen hoe ze komen op deze twee formules tussen haakjes? Ik snap niet waar ze deze vandaan hebben gehaald, en dan specifiek de tweede formule (als ik het goed zeg) tussen haakjes.
A
13-2-2024

Antwoord

Het gaat om deze opgave:

De breedte van het karton is b. Langs de lange zijde worden twee stroken met breedte x omhoog gevouwen voor de opstaande zijkanten, dan blijft voor de breedte van de doos over:

breedte doos = b-2x

De doos is vierkant, dus geldt ook:

lengte doos = b-2x

De hoogte wordt x. Gegeven is: de inhoud is 100. Met de formule voor inhoud kunnen we dan b uitdrukken in x:

In figuur 11 van de opgaven zie je dat de lengte l van het karton twee keer de lengte van de doos is, plus drie keer de hoogte x:

Vul de gevonden uitdrukking voor b in deze formule in:

De oppervlakte A van het karton is breedte $\times $ lengte, ofwel b $\times $ l:

Hiermee is de formule gevonden waar je naar vroeg.

Is hiermee het probleem opgelost?
GHvD
14-2-2024

Re: Wat is differentiëren?

Het woord stijlheid bestaat niet, het moet steilheid zijn.
Jan
5-9-2024

Antwoord

Dat was me nog niet opgevallen, maar geregeld.
Bedankt!
WvR
6-9-2024