Componenten van een kracht

Hallo,
Een driehoek ABC hangt aan een vertikale muur via BC met hoek B van 45° en hoek C van 60° graden tov de muur.
Aan punt A hangt een gewicht van 180 newton.
Bereken de grootte van de twee componenten van dat gewicht die langs AB en BC worden uitgevoerd.
Ik moet dus de kracht ontbinden in x- en y-component.
Voor de x-richting is dat: FAB,x +FAC,x = 0 omdat de horizontale krachten 0 zijn.
Voor de vertikale aarzel ik tussen FAB,y − FAC,y = −180 en FAB,y + FAC,y = −180. Kracht AB werkt naar boven, maar ik welke richting werkt kracht AC?
Als het FAB,y − FAC,y = −180 is wordt het FAB · sin 45◦ − FAC · sin 30◦ = −180◦, anders FAB · 45◦ + FAC · sin 30◦ = −180◦
Bedankt.
Valerie

2de graad ASO - maandag 5 augustus 2024

Antwoord

Hallo Valerie,

Voor het bepalen van de richting van een kracht is het steeds erg belangrijk dat je denkt aan de krachten die door de omgeving op een voorwerp worden uitgeoefend, anders raak je helemaal in de war. In dit geval gaat het dus om de krachten die door de muur en het gewicht op de driehoek worden uitgeoefend. Deze krachten moeten met elkaar in evenwicht zijn.
In de figuur hieronder zie je de driehoek waarop het gewicht van F_A=180 newton werkt. Bij de driehoek heb ik de krachten F_B en F_C getekend die door de muur op de punten B en C van de driehoek werken:



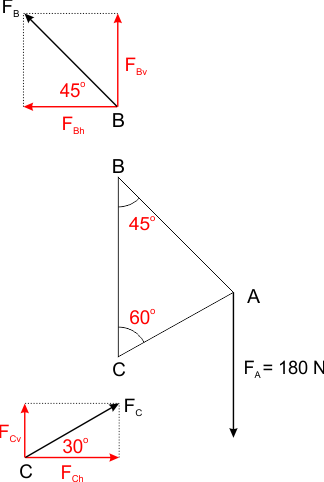
De verticale componenten F_Bv en F_Cv werken omhoog, want deze moeten de kracht F_A compenseren. (Verwar deze krachten niet met de kracht van de driehoek op de muur, deze zijn naar beneden gericht). In de figuur zie je dat moet gelden:

F_B·sin(45°) + F_C·sin(30°) = 180

De horizontale componenten van F_A en F_C moeten samen nul zijn, dus geldt:

F_B·cos(45°) = F_C·cos(30°)

In punt B werkt kracht van de muur op de driehoek van punt A af, de kracht in zijde AB is dus een trekkracht.
In punt C werkt de kracht van de muur op de driehoek naar punt A toe, de kracht in zijde AC is dus een drukkracht.

maandag 5 augustus 2024

©2004-2024 WisFaq