Limiet recursieve functie

f(n) is gedefinieerd als volgt: voor n=0 geld f(n) = 1, anders is f(n) gelijk aan f(n-1)+¹/_f(n-1), nu is mijn vraag: 'Convergeert deze functie? Zo ja, wat is lim_{n \to \infty} (f(n)) dan?'

Heel erg bedankt voor uw hulp!

Oliver
1ste graad ASO-TSO-BSO - zondag 24 maart 2024

Antwoord

Merk allereerst op dat de rij stijgend is:

f(n)=f(n-1)+\frac1{f(n-1)} > f(n-1)

Teken de webgrafiek van de getallenrij die je zo krijgt:

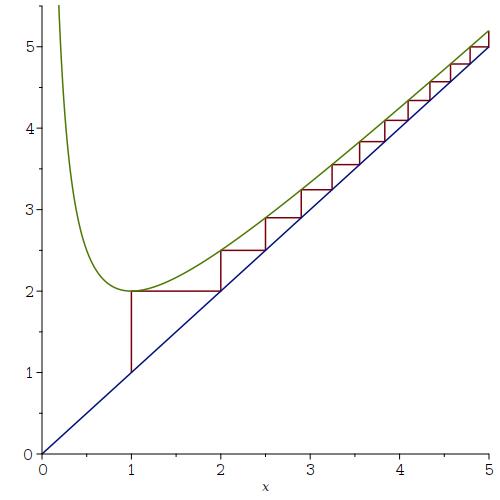
Dat suggereert dat de waarden onbeperkt toenemen, en dat de rij divergeert.

Inderdaad: als de rij zou convergeren naar L dan zou L aan de vergelijking L=L+\frac1L moeten voldoen, maar die heeft geen oplossing, dus \dots

kphart
zondag 24 maart 2024

Re: Limiet recursieve functie

©2001-2025 WisFaq