Modulus vergelijking

Hoi,

Kan iemand mij helpen de volgende modulus vergelijking op te lossen?
|6 – x²| = |x| + 2

Ik weet dat ik tot 4 oplossingen moet komen maar zie niet helemaal hoe.

Alvast bedankt!

Jes
Leerling bovenbouw havo-vwo - dinsdag 17 januari 2023

Antwoord

Je kunt 4 gevallen onderscheiden:


$
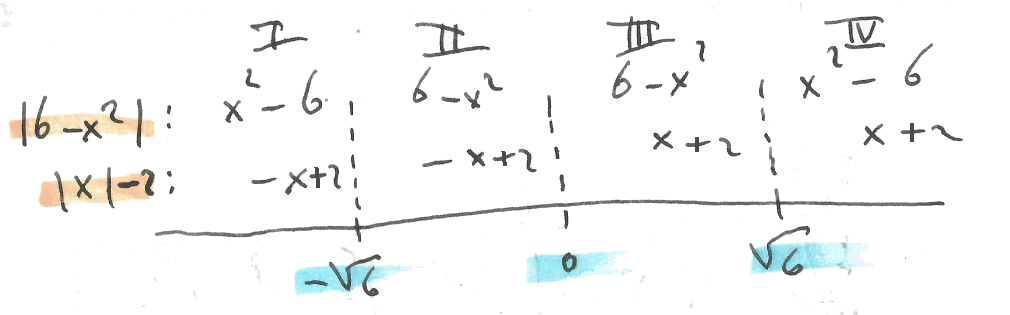
\left| {6 - x^2 } \right|
$ geeft:

$
x^2 - 6
$ voor $
x $<$ - \sqrt 6 \vee x $>$ \sqrt 6
$

$
6 - x^2
$ voor $
- \sqrt 6 \leq x \leq \sqrt 6
$

Evenzo $
\left| x \right|
$ geeft $
- x+2
$ voor $
x $<$ 0
$ en $
x+2
$ voor $
x \geq 0
$.

Je moet dan 4 vergelijkingen oplossen waarbij je steeds moet controleren of de gevonden oplossingen wel of niet in het interval liggen:

$
\eqalign{
& I\,\,x^2 - 6 = - x + 2 \cr
& II\,\,\,6 - x^2 = - x + 2 \cr
& III\,\,\,6 - x^2 = x + 2 \cr
& IV\,\,\,x^2 - 6 = x + 2 \cr}
$

Voor I ziet dat er dan zo uit:

$
\eqalign{
& x^2 - 6 = - x + 2 \cr
& x^2 + x - 8 = 0 \cr
& ABC - formule \cr
& x = - \frac{1}
{2} - \frac{1}
{2}\sqrt {33} \vee x = - \frac{1}
{2} + \frac{1}
{2}\sqrt {33} \,\,(v.n.) \cr}
$

De tweede oplossing valt niet in het interval van I dus die doet niet mee. Eén oplossing gevonden. Nu kun je de andere 3 oplossingen bij II, III en IV ook wel vinden, denk ik.

Succes!

• 9. Vergelijkingen met absolute waarde oplossen

dinsdag 17 januari 2023

©2001-2024 WisFaq