De hoogte van een toren

Ik begrijp niet goed hou je dit vraagstuk kan oplossen zonder rekenmachine:

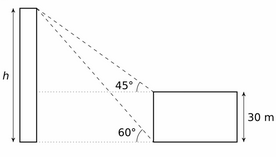
Een toren staat naast een gebouw van 30 m hoog. Vanop het gelijkvloers van het gebouw ziet men de top van de toren onder een hoek van 60^o en vanop het dak ziet men deze onder een hoek van 45^o met de horizontale.

• Hoe hoog is de toren?

George
3de graad ASO - zondag 19 juni 2022

Antwoord

Je hebt te maken met twee rechthoekige driehoeken. Neem even aan dat de afstand van het gebouw tot de toren gelijk is aan $a$. Er geldt:

$
\eqalign{
& \tan (60^\circ ) = \frac{h}
{a} \cr
& \tan (45^\circ ) = \frac{{h - 30}}
{a} \cr}
$

Bovendien:

$
\eqalign{
& \tan (60^\circ ) = \sqrt 3 \cr
& \tan (45^\circ ) = 1 \cr}
$

Twee vergelijkingen met twee onbekenden? Zou het dan lukken?

Naschrift
Of meteen in de 60^o-driehoek:

$
\eqalign{
& \tan (60^\circ ) = \frac{h}
{{h - 30}} \cr
& \frac{h}
{{h - 30}} = \sqrt 3 \cr}
$

zondag 19 juni 2022

©2001-2024 WisFaq