Bewijs voor de constructie van een regelmatige vijfhoek

Op het web heb ik reeds een aantal mogelijkheden gevonden om een vijfhoek in een cirkel te construeren. Doch bij geeneen van deze mogelijkheden stond een bewijs waarom die bepaalde constructie weldegelijk een juiste (regelmatige) vijfhoek leverde. Mijn vraag ios nu of u (jullie) weten waar ik een bewijs kan vinden waarom een bepaalde (maakt niet uit dewelke) constructie weldegelik een regelmatige vijfhoek levert.
Ik hoop dat mijn vraag nu duidelijk is.
alvast bedankt

bart e
Student Hoger Onderwijs België - woensdag 19 maart 2003

Antwoord

Ik heb maar niet gezocht op internet. Waar zo'n bewijs staat? Hieronder!



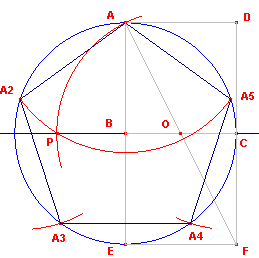
In de hierboven staande figuur is BC = 1, terwijl O het midden is van BC.
ABCD en BEFC zijn vierkanten.
Allereerst de constructie (die eigenlijk erg eenvoudig is).
De cirkel (O, OA) snijdt de drager van het lijnstuk BC in het punt P.
De cirkel (A, AP) snijdt de omcirkel in de punten A2 en A5, samen met A zijn dat hoekpunten van de regelmatige vijfhoek.
De hoekpunten A3 en A4 kunnen we vinden met de cirkels (A2, AA2) en (A5, AA2) of als symmetriepunten van A2 en A5 tov. het punt B.
Berekeningen (bewijs).
Nu is OA = OP = ¹/₂5
Door de constructie is AP = AA2
We moeten nu aantonen, dat AA2 een zijde is van een regelmatige 5-hoek.
Volgens de cosinusregel in driehoek AOP is
AP² = (¹/₂5)² + (¹/₂5)² - 2(¹/₂5)².cos(AOP)
Die laatste cosinus is gelijk aan 1/5.
Na enig rekenwerk vinden we dan:
AP² = 2¹/₂ - ¹/₂5
Voor de zijde a van een regelmatige 5-hoek geldt
a² = 2 - 2 cos(72°).

En het bewijs dat dan AP = a laat ik aan de vragensteller.

Voor wat meer informatie zie onderstaande webpagina.

Zie Wortel 5 en de vijfhoek

woensdag 19 maart 2003

Re: Bewijs voor de constructie van een regelmatige vijfhoek

©2001-2024 WisFaq