Als je het hebt over:
...dan is het antwoord: jazeker! Daar zit wel een redering achter.
Laten we maar eens kijken naar de afleiding van de formule:
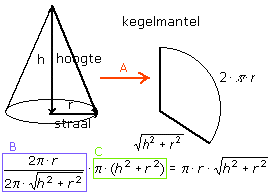
De kegelmantel laat zich uitvouwen als een cirkelsegment (zie A). De vraag is dan: wat is de oppervlakte van dit cirkelsegment?
De straal van deze cirkel is gelijk aan √(h2+r2). De oppervlakte van de hele cirkel zou $\pi$·(√(h2+r2))2=$\pi$·(h2+r2) zijn (zie C).
Het is echter geen cirkel, maar een cirkelsegment. Welk deel heb je nodig? De omtrek van de hele cirkel zou 2$\pi$√(h2+r2) zijn (zie de noemer bij B). Het cirkelboogje van het cirkelsegment is 2$\pi$r (zie de teller van B), dus het cirkelsegment is het 'zoveelste gedeelte' van de hele cirkel. En dat 'zoveelste gedeelte' is dan precies de uitdrukking bij B.
Als je vervolgens B en C vermenigvuldigt krijg je precies de oppervlakte van het cirkelsegment, dus de oppervlakte van de kegelmantel. Daarbij gebruik je dus de formules voor omtrek en oppervlakte van een cirkel.
Hopelijk is het duidelijk, anders horen we het wel.
vrijdag 27 december 2002
Re: Afleiden van de formule voor de oppervlakte kegel
