Twee identieke vazen en een blauwe knikker

Twee identieke vazen (V₁ en V₂). V₁ bevat 3 rode, 5 witte en 7 blauwe ballen. V₂ bevat 7 rode, 5 witte en 3 blauwe ballen. Iemand trekt uit een willekeurige vaas aselect een bal. De getrokken bal is blauw. Wat is de kans dat deze bal uit V₁ getrokken is?

Sjouk
Student hbo - zaterdag 9 juni 2007

Antwoord

Zoiets gaan handig met een boomdiagram:



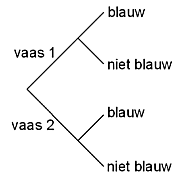
Bereken P(vaas 1 en blauw) en P(vaas 2 en blauw). De voorwaardelijke kans P(vaas 1 | de knikker is blauw) is dan gelijk aan:

$
\eqalign{ \frac{{P(vaas\,\,1\,\,en\,\,blauw)}}
{{P(vaas\,\,1\,\,en\,\,blauw) + P(vaas\,\,2\,\,en\,\,blauw)}}}
$

Of ook:

We onderscheiden twee gebeurtenissen:

A: de knikker is afkomstig uit vaas 1
B: de getrokken knikker is blauw

Er geldt: $
\eqalign{P\left( {A|B} \right) = \frac{{P\left( {A\,\,en\,\,B} \right)}}
{{P\left( B \right)}}}
$

Als het goed is zul je zien dat dit hetzelfde is als het eerstgenoemde hierboven.

Zie ook 4. Voorwaardelijke kans

zondag 10 juni 2007

Re: Twee identieke vazen en een blauwe knikker

©2001-2024 WisFaq