Bewijs inhoudsformule van piramide

Kunt u ons een begin stap geven om de formule van 1/3gh te bewijzen zonder deze formule te gebruiken. we maken gebruik van een piramide met als grondvlak een driehoek met 60° en een hoogte van 6 cm. de driehoek van het grondvlak past in een cirkel met r= 5cm. We willen dus bewijzen dat als we de deze piramide in een kubus doen dat dan de formule voor de rest ruimte gelijk is aan 2/3gh.
Ik hoop dat u ons voor een gedeelte kunt helpen.
Met vriendelijke groeten,

T. Hui
Leerling bovenbouw havo-vwo - vrijdag 11 oktober 2002

Antwoord

Hoi,

Ik denk dat je het jezelf moeilijk maakt door die piramide met driehoekig grondvlak in een kubus te willen stoppen. Je zou dan moeten overgaan van een (gelijkzijdige) driehoek op een vierkant met dezelfde oppervlakte. Dit kan meetkundig, maar het zal niet bijdragen om de volumeformule voor de piramide beter te begrijpen.
(de zijde van een dergelijk vierkant vierkant is de middelevenredige tussen a = halve basis en b =hoogte van driehoek. Je kan die construeren als de hoogtelijn van een rechthoekige driehoek met schuine zijde a+b in een punt dat deze schuine zijde in verhouding a/b verdeelt. Dit is het snijpunt van de halve cirkel op a+b en de loodlijn in het punt dat de twee lijnstukken verbindt)

We kunnen ons dus beter beperken tot een prisma (ipv een kubus) met hetzelfde grondvlak en de zelfde hoogte als de piramide.

Continue gesloten vlakke krommen kunnen willekeurig dicht benaderd worden door een veelhoek, zodat daarmee de formule geldt voor elke continue vlakke kromme zodra we ze voor veelhoeken kunnen bewijzen.



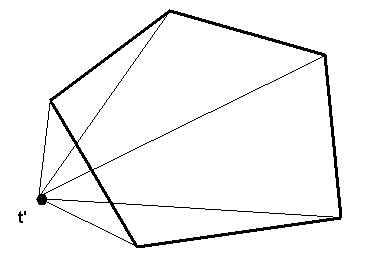
(figuur 1)
De veelhoek in figuur 1 is het grondvlak van een piramide. We kiezen een willekeurige richting niet-evenwijdig met het grondvlak. De projectie van het toppunt t noemen we t’. Elke zijde van de veelhoek, verbonden met t’ vormt een driehoekje. We kunnen het oppervlak van het grondvlak samenstellen als een som of verschil van die driehoekjes (afhankelijk van of t’ langs de ‘binnenkant’ ligt van de grondlijn of niet). Elk driehoekje vormt het grondvlak van een kleine piramide met top t met een driehoekig grondvlak. Deze driehoekige piramides kunnen op dezelfde manier als de grondvlakken samengesteld worden tot het volume van de eerste piramide. Het volstaat dus dat we de formule bewijzen voor piramides met een driehoekig grondvlak. Dit is precies waar je opdracht begint.



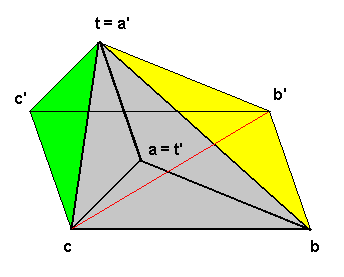
(figuur 2)
In de tweede figuur vinden we een driehoekige piramide met top t en grondvlak abc. Als projectierichting kiezen we ta, zodat p(t)=t’ =a. We tekenen het vlak door t evenwijdig aan vlak abc. We kiezen a’, b’ en c’ zodat p(a’)=a, p(b’)=b en p(c’)=c. We bekijken nu prisma P:abca’b’c’ en zien dat het samengesteld is uit 3 driehoekige piramides: P1:abca’, P2:a’cc’b’ en P3:a’bb’c (P1: grijs, P2: groen en P3: geel).

Uit de constructie zien we dat P1 in P2 overgaat door een asspiegeling rond de rechte die [ac’] en [bb’] middendoor snijdt. P1 en P2 hebben dus hetzelfde volume. Op dezelfde manier gaat P1 in P3 over door een asspiegeling rond c en het midden van [a’b]. Ook P1 en P3 hebben dus hetzelfde volume. Het prisma heeft een volume G.h. Het volume van piramide abct is dus G.h/3 (QED).

Met 'ZOEKEN' vind je wellicht nog heel wat nuttige informatie op deze site...
Laat je weten of je hiermee geholpen bent?

Groetjes,
Johan

andros
maandag 21 oktober 2002

©2001-2024 WisFaq