Ik begrijp het... laten we eens een voorbeeld doen.
Los op: x3-9x2+31x-39=0
Als de grafiek tekent met je GR:
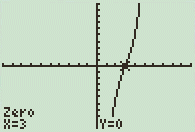
Het lijkt er op dat x=3 een oplossing is. Dus gaan we weer 'gezellig' een staartdeling maken:x-3/x³-9x²+31x-39\x²-6x+13
x³-3x²
------ -
-6x²+31x-39
-6x²+18x
-------- -
13x-39
13x-39
------ -
0
We zien:
x3-9x2+31x-39=(x-3)(x2-6x+13)
We proberen nu x2-6x+13 te ontbinden... (je kent misschien de som-produktmethode nog wel... twee getallen zoeken die vermenigvuldigd 13 zijn en opgeteld -6 zie Vergelijkingen oplossen m.b.v. ontbinden in factoren)
Dat lukt dus niet... dan maar de ABC-formule:
D=(-6)2-4·1·13=36-52=-16
'Normaal' (dat wil zeggen als je in $\mathbf{R}$ probeert deze vergelijking op te lossen) stop je dan met de opmerking: 'geen oplossingen'. Je bedoelt dan eigenlijk geen reële oplossingen.
Maar wij weten beter...
We vullen de ABC-formule gewoon verder in zoals we dat altijd al deden:
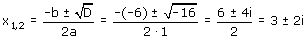
Kijk maar eens goed... we gebruiken i2=-1
√(-16)=√(4·-1)=√4 · √(-1)=2i
('populair gezegd': √(-1)=i)
En zo gaat dat dan zo'n beetje.
Er is nog een aardig aspect... wat ik toch even wil vermelden...
Je kunt nu schrijven:
x3-9x2+31x-39=(x-3)(x+2i-3)(x-2i-3)
Maar hoe kan het dat het vermenigvuldigen van twee complexe getallen aan de rechter kant geen complexe getallen oplevert aan de linker kant?
(x+2i-3)(x-2i-3)=x2-2ix-3x+2ix+4-6i-3x+6i+9
En zoals je ziet vallen alle termen met complexe getallen er in precies tegen elkaar weg!
x2-2ix-3x+2ix+4-6i-3x+6i+9=x2-3x+4-3x+9=x2-6x+13
(het klopt ook nog...)
Stel je nu eens voor dat je een derdegraadsvergelijking hebt (met reele coefficienten) waarbij je 2 reele oplossingen en 1 complexe oplossing krijgt. Zou dat kunnen kloppen denk je? Waarom niet?
maandag 18 augustus 2003
Dit is een reactie op vraag 13479 