\require{AMSmath}

Formule loodrechte lijn opstellen normaalvector

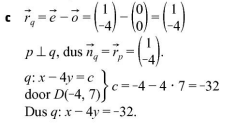
De vraag:
Stel een vergelijking op van de lijn p door het punt D(-4, 7) die loodrecht staat op de lijn q door de punten O en E(-1, 4).
Ik had dit als antwoord ((getal getal) zonder komma is een vector):
rq = (1 -4) - (0 0) = (1 -4)
p loodrecht op q dus rp = (4 1)
dan p: 4x + y = c = 4(-4) + 7 = -9
dus p: 4x + y = -9

In de uitwerkingen wordt simpelweg dit gezegd:
rq = (1 -4)
p loodrecht op q dus nq = rp = (1 -4) en dan rekenen ze daarmee verder, maar omdat het loodrecht is moet je toch de normaalvector van q pakken en dat is dan toch gewoon de richtingsvector naar links of rechts draaien? De normaalvector kan toch niet hetzelfde zijn als de richtingsvector?

Klopt de uitwerking gewoon niet of doe ik wat fout?

Leerling bovenbouw havo-vwo - dinsdag 18 maart 2025

Antwoord

Zowel de gegeven uitwerking als de jouwe zijn niet foutloos.

In de gegeven uitwerking zijn bij het opschrijven letters verwisseld denk ik.
Dat \vec r_p=\vec n_q klopt maar dan lijkt het of p en q omgewisseld zijn. Er moet staan \vec n_p=\vec r_q=\binom{1}{-4}.
De laatste drie regels van die uitwerking geven nu juist een vergelijking voor p.

In jouw uitwerking gaat er ook iets mis: je hebt gelijk dat \vec r_p=\binom{4}{1}, maar, zoals je zelf zegt \vec r_p is niet een normaalvector voor p, daar moet je nu juist \binom{1}{-4} voor hebben en dan krijg je de vergelijking als in de gedrukte uitwerking.

©2004-2025 WisFaq