\require{AMSmath}

Dubbele integraal opstellen mbv poolcoördinaten

ik, heb moeite om de grenzen van theta te vinden bij deze specifieke opgave, zou iemand kunnen helpen?

(3 punten) Beschouw het gebied G ingesloten tussen de
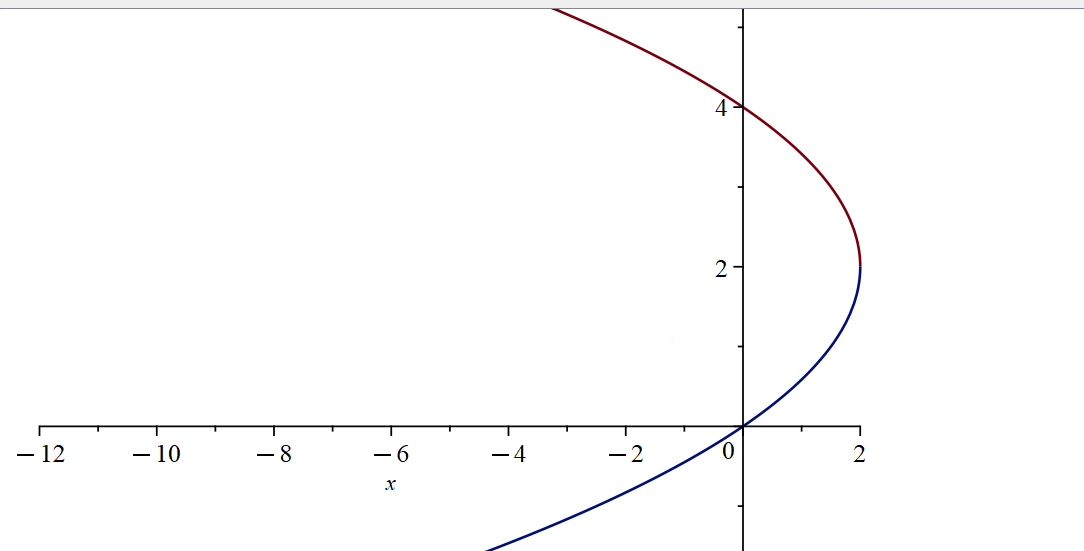
Y-as en de kromme met vergelijking 2·x= -y²+4·y

Bereken de oppervlakte van dit gebied door de integraal te schrijven in poolcoördinaten als

opp(G)=∫ab(∫cdF(r,θ) dr)dθ
opp(G)=∫

i. Geef de grenzen voor de integraal over r
r: ______
ii. Geef de grenzen voor de integraal over θ
θ: ______
iii. Geef de numerieke uitkomst van de integraal: ______

Student universiteit België - zondag 16 maart 2025

Antwoord

i) substitueer x=r\cos\theta en y=r\sin\theta in de vergelijking herschrijf het resultaat in de vorm r=\ldots; dit geeft de bovengrens voor r, de ondergrens is makkelijk.

ii) de bovengrens is \frac\pi2; voor de ondergrens bereken je de helling van de parabool in het punt (0,0).

iii) dit zou niet moeilijk moeten zijn met een geschikt programma, Maple bijvoorbeeld

©2004-2025 WisFaq