\require{AMSmath}

Vraagstuk oplossen met stelling van Pythagoras

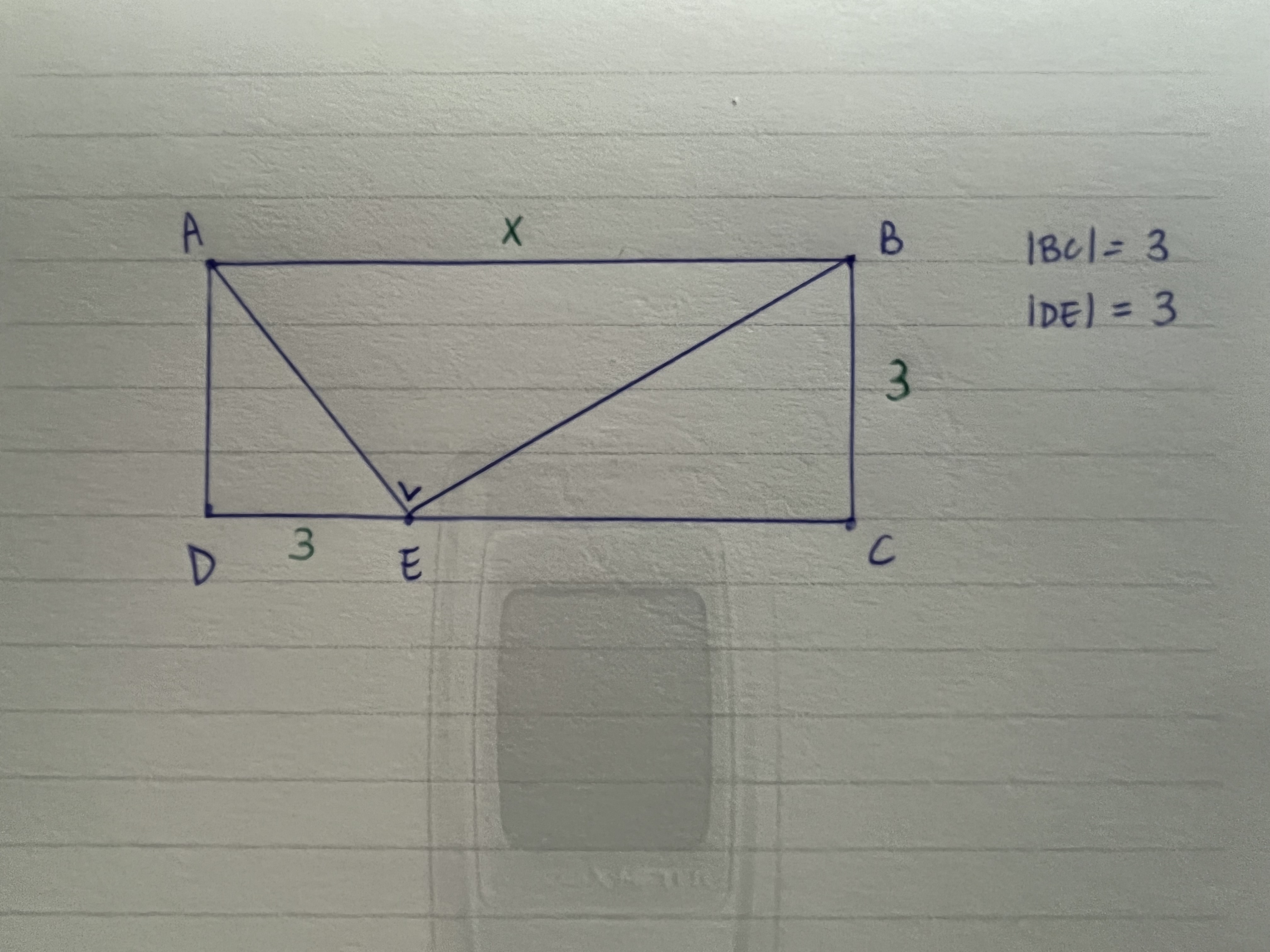
In een rechthoek ABCD is een rechthoekige driehoek AEB (met E de rechte hoek) getekend. Gegeven is dat BC = 3 en DE = 3. Nu vragen ze om de lengte van AB (of x) te berekenen.

Ik ben er vanuit gegaan dat AD = 3 (overstaande zijde in een rechthoek zijn gelijk).

In driehoek ADE heb ik de stelling van Pythagoras toegepast om zijde AE te berekenen. Ik kom 3 $\sqrt{}$ 2 uit.

Nu zit ik echter vast omdat ik niet weet hoe ik verder moet. Ik dacht EC = x - 3, om zo de stellig van Pythagoras toe te passen in driehoek EBC. Maar dit wordt dan te complex

2de graad ASO - zondag 1 december 2024

Antwoord

Hallo Lien,

Laat je niet te snel ontmoedigen: met jouw aanpak verwacht je iets complex, maar dat valt erg mee. Gewoon netjes uitwerken:

In driehoek EBC geldt:

BE² = EC² + 3²
BE² = (x-3)² + 3²
BE² = x²-6x+9 + 9
BE² = x²-6x+18

In driehoek AEB geldt:
x² = BE² + AE²

met BE²=x²-6x+18 en AE²=(3 $\sqrt{}$ 2)²=18 wordt dit:

x² = x²-6x+18 + 18
x² = x²-6x+36
6x=36
x=³⁶/₆=6

Overigens kan je dit ook meetkundig berekenen:
AD = DE = 3, dus driehoek ADE is gelijkbenig. Dan geldt: hoek DAE = hoek DEA. Deze hoeken samen zijn 180°-90°=90° (hoekensom in driehoek ADE), dus:
hoek DAE = hoek DEA = 45°.

Dan vind je voor hoek BEC:
Hoek BEC = 180°-45°-90° = 45° (Hoek DEC is gestrekte hoek, dus 180°).
Hoek BEC is dan ook 45° (hoekensom in driehoek EBC), dus driehoek EBC is weer gelijkbenig met EC=BC.

Conclusie: EC=3, dus DC=3+3=6, dus x=6.

OK zo?

©2004-2024 WisFaq