\require{AMSmath}

Voorwaardelijke kans

Er werd een onderzoek opgezet naar de werkzaamheid van een nieuwe test voor het opsporen van een parasiet op beukenbomen. Elke beuk reageert positief of negatief op de test.
De bevindingen van het onderzoek zijn de volgende:
14% van de beuken test positiet,
2% van de beuken test positief, maar heeft de parasiet niet,
4% van de beuken test negatief, maar heeft toch de parasiet.
Wat is de kans dat, als een beuk de parasiet heeft, de beuk ook positief zal testen?

3de graad ASO - maandag 24 juni 2024

Antwoord

Hallo Sirine,

Zet de gegevens in een kruistabel:



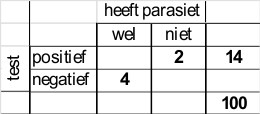
De lege cellen kan je nu berekenen, bijvoorbeeld:
14% test positief, dus 100-14=86% test negatief. In de cel tussen 14 en 100 noteer je dus 86. Vul op deze manier de tabel helemaal in.

Dan de kans dat, als een beuk de parasiet heeft (dus: 16%), de beuk ook positief zal testen (dat is 12%). Deze kans is zodoende ¹²/₁₆.

OK zo?

©2004-2024 WisFaq